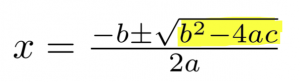
A few weeks ago, before spring break we learned about the discriminant. This is used in the unit of quadratics and it is a portion of the quadratic formula. The discriminant is able to tell us the amount of solutions it will have.

# of solutions: 

• positive number : 2 solutions
• negative number: no solution
• equal to zero : 1 solution

. ex.

1. determine a, b, and c from the equation:    a = 5    b= -9    c = 4
2. enter into the discriminant formula:

• 
• 
• 
• = 1

This number is positive, therefore, it has two solutions

ex2/ $latex x^2 + 8x + 16 = 0

1. a = 1,   b = 8,   c = +16
2. 
3. 
4. 
5. = 0
6. (equal to zero) 1 solution

   

ex3/ $latex -2x^2 + 3x – 10 = 0

1. a= -2,   b = 3,    c= -10
2. 
3. 
4. 
5. = -71
6. (negative number) No solution

This is how you would find the discriminant, as well as finding how many solutions it has. Using this can also help determine if the answer will be a rational or irrational number.