Tag Archives: Trigonometry

Grade 11, Math 11

Week 17 Pre Calculus 11: Sine Law

Leave a comment

Image result for sine law cartoon jokes

Hey there, thanks for coming back to my blog!! This week in Pre Calculus 11 we learned two very important formulas that will make solving triangles so much easier. I am so thankful that I learned how to use this. If you stay tuned you too, will learn the secrets of trigonometry. Super helpful, keep reading.

Mathematicians are very organized and you will see them use CAPITAL LETTERS, the Theta symbol (\theta), small case letters, and x’s now and then

  1. The capital letters in a triangle will represent each angle of a triangle.
  2. ( \theta ) which will represent the unknown angle.
  3. small case letters will represent the sides of the triangle. Neat enough the small letter represent the opposing side of the big letter.
  4. X represents the unknown angle or side length.

This is the Sine law

\frac{a}{ Sin A} = \frac{b}{Sin B} = \frac{c}{Sin C}
  • If you are looking for a side length it is easier to put the side lengths (small letters on the top. You can reciprocate the whole Sin law if you are looking for an angle.

EXAMPLE: Triangle ABC

Find the side length of AB (also known as c)

Step 1: Find the given angles and side lengths

  • AB (c) = x
  • BC (a) = unknown
  • AC (b) = 5.0 cm
  • A = 180 - 80 - 30 = 70^o
  • B = 80^o
  • C = 30^o

Step 2: Fill in the Sine Law

  • \frac{a}{ Sin A} = \frac{b}{Sin B} = \frac{c}{Sin C}
  • \frac{a}{ Sin 70^o} = \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}

Step 3: Find out which equation to use

\star We need side c, and we have the numerator and denominator of \frac{b}{Sin B}. So we can use…

  • \frac{b}{Sin B} = \frac{c}{Sin C}
  • \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}

Step 4: Solve for c

  • \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}
  • Sin 30^o\cdot \frac{5.0cm}{Sin 80^o} = x
  • x = 2.5 cm

Final Answer: Side AB (side c) = 2.5cm

Trying to find an Angle using Sine Law.

Steps:

  1. Use the reciprocated version of the Sine Law \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}
  2. Find the given angles and side lengths
  3. Fill in the Sine Law
  4. Find which equation to use
  5. Solve
  6. To get theta (\theta) by itself you have to use inverse sine (2nd function sine)
  7. Check which quadrants they are in to make sure that you get the correct angle.

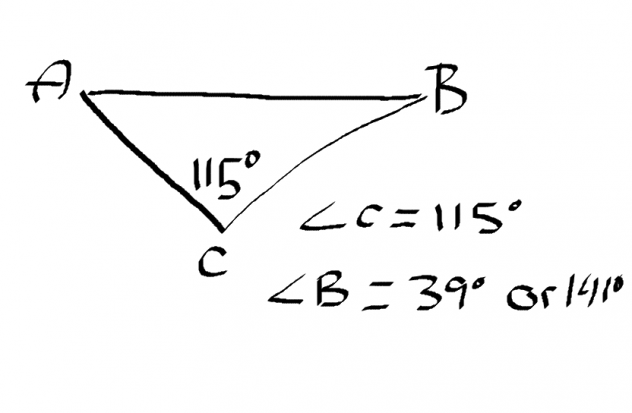
Example: Find Angle B

Step 1: Use the reciprocated version of the Sine Law \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}

Step 2: Find the given angles and side lengths

  • AB (c) = 10 cm
  • BC (a) = unknown
  • AC (b) = 7.0 cm
  • A = unknown
  • B = \theta
  • C = 150^o

Step 3: Fill in the Sine Law

  • \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}
  • \frac {Sin A}{a} = \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}

Step 4: Find which equation to use..

\star I have enough information to use .

  • \frac {Sin B}{b} = \frac {Sin C}{c}
  • \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}

Step 5: Solve

  • \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}
  • Sin B= \frac {Sin 115^o}{10 cm}\cdot 7.0 cm
  •  B= Sin^{-1}( \frac {Sin 115^o}{10 cm} \cdot 7.0 cm)
  • \angle B \doteq 39^o

Step 6: Check which quadrants they are in to make sure that you get the correct angle.

\star Using the cast rule

This means that Sin 39^o can be in either Quadrant 1 or 2 Because it will be positive where All and Sine is.

\star The reference angle in both Q1 and Q2 would be 39^o

\star The rotation angle in Q1 would be…

  • 0 + 39 = 39^o

\star The rotation angle in Q2 would be…

  • 180 – 39 = 141^o

\angle B can either be 39^o or 141^o

But since 141^o + 115^o = 256^o and exceeds the maximum amount a triangle can be with all three angles added together to make 180^o \angle B \neq 141^o

\therefore \angle B = 39^o and not 141^o

This is how you would use the Sine Law in Trigonometry