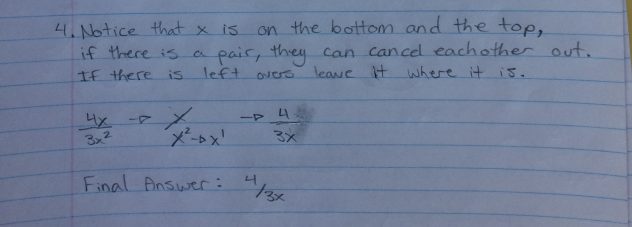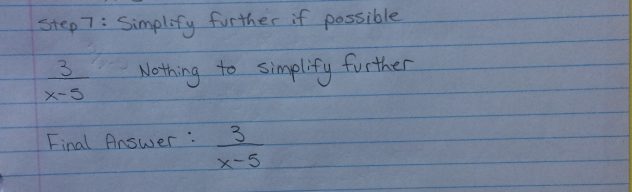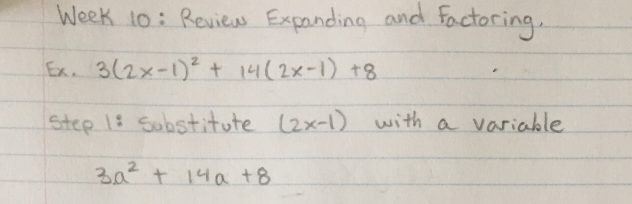Category Archives: Math 11

Grade 11, Math 11

Top 5 Things I learned During Pre-Calculus 11

Leave a comment

Related image

This week will be my very last blog post for Pre-Calculus 11. I have learned so many things and so many skills from taking this course and I’m really happy I chose it. Some of my favorite parts of this class was getting to sit with multiple people and learn from them. I liked learning new techniques and hearing ideas and helping others, which helped me become a better teacher and helped me understand things better. To be honest I learned that I like writing blog posts, for me it is very time consuming but it is very useful and I can always go back and look at my work and review. It is a skill that I need to have because I need have to be able to transfer what I’m thinking to others and be able to interpret how to do things. I think blog posts will help me on my numeracy assessment because I will have to be able to write down what I’m thinking and why I am thinking in that way. Anyway, This whole post is to share what the top 5 things I learned in this class, so I should get on that. 

Number 1: My allowance

In our first chapter we learned about geometric series. I liked this the most because I learned how to trick my parents with my allowance. It didn’t really work for that long because they realized that they would be giving me more money, and I mean a lot more money than I would normally get. But I think that it was cool that I was at least one step ahead of the game for once. I could have been rich in a month. How exciting 😀

Number 2: Improving My Blogging Capabilities 

During this semester, I think I really improved my blog posting skills. I learned some new ways to make my blog posts look pretty dang good. I tried really hard when working on my blog posts because if I got stuck on something I could always go back and look at my previous work. It has also helped me so much with reviewing for test and finals. This is also a way for me to be able to teach others and has helped me learn how to teach others, which is a very valuable skill to have.

Number 3: Learned something that connected with socials

I always wondered what pre-calculus could help with outside of class. It too, connects with sequences and series unit. In Socials, we learned a lot about population, and the downfalls with it. Our most common debating topic was if the world was over populated or not. We came to learn that Thomas Malthus wrote an essay on how food production is arithmetic, and population growth is geometric. I learned that he believed that we would one day become overpopulated because we would run out of land to produce food and at the same time run out of room for everyone to live. I thought this was a pretty cool connection. 

Number 4: Better Studying Habits

Personally, I learned what was best for me when I Study. Math is a subject where you actually have to do work to learn and understand. For me I really like to break down what I was doing to truly understand. That’s is why I worked so hard in my blog posts. I like to see every step so I know exactly what to do and then I can take shortcuts after. I also learned that it’s not a subject where you can just wait for the day before a test to cram everything in. Working a little bit after school everyday helped me dramatically. 

Number 5: How to Work with Others

I think this was a very important thing for me to get used to because sometimes I don’t really want to ask for help. But with working with my peers I learned that its okay to not know how to do something, because when you ask you give the chance for two people to get better. I really enjoyed working with multiple people in my class especially when switching up the table groups because I got to know almost everyone and how to do things in a new way. I think that I got better when working with others because I wasn’t as afraid of my peers when I got to know someone new.

Overall I loved Pre-Calculus 11. It was challenging at times, but I feel like I pushed through and did very well. I am really proud of my effort and positivity this year, as well as my overall performance. I learned many things, not just about math but things outside of class. I had lots of fun and I am really looking forward to Pre-calculus 12 🙂

 

 

Grade 11, Math 11

Week 17 Pre Calculus 11: Sine Law

Leave a comment

Image result for sine law cartoon jokes

Hey there, thanks for coming back to my blog!! This week in Pre Calculus 11 we learned two very important formulas that will make solving triangles so much easier. I am so thankful that I learned how to use this. If you stay tuned you too, will learn the secrets of trigonometry. Super helpful, keep reading.

Mathematicians are very organized and you will see them use CAPITAL LETTERS, the Theta symbol (\theta), small case letters, and x’s now and then

  1. The capital letters in a triangle will represent each angle of a triangle.
  2. ( \theta ) which will represent the unknown angle.
  3. small case letters will represent the sides of the triangle. Neat enough the small letter represent the opposing side of the big letter.
  4. X represents the unknown angle or side length.

This is the Sine law

\frac{a}{ Sin A} = \frac{b}{Sin B} = \frac{c}{Sin C}
  • If you are looking for a side length it is easier to put the side lengths (small letters on the top. You can reciprocate the whole Sin law if you are looking for an angle.

EXAMPLE: Triangle ABC

Find the side length of AB (also known as c)

Step 1: Find the given angles and side lengths

  • AB (c) = x
  • BC (a) = unknown
  • AC (b) = 5.0 cm
  • A = 180 - 80 - 30 = 70^o
  • B = 80^o
  • C = 30^o

Step 2: Fill in the Sine Law

  • \frac{a}{ Sin A} = \frac{b}{Sin B} = \frac{c}{Sin C}
  • \frac{a}{ Sin 70^o} = \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}

Step 3: Find out which equation to use

\star We need side c, and we have the numerator and denominator of \frac{b}{Sin B}. So we can use…

  • \frac{b}{Sin B} = \frac{c}{Sin C}
  • \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}

Step 4: Solve for c

  • \frac{5.0cm}{Sin 80^o} = \frac{x}{Sin 30^o}
  • Sin 30^o\cdot \frac{5.0cm}{Sin 80^o} = x
  • x = 2.5 cm

Final Answer: Side AB (side c) = 2.5cm

Trying to find an Angle using Sine Law.

Steps:

  1. Use the reciprocated version of the Sine Law \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}
  2. Find the given angles and side lengths
  3. Fill in the Sine Law
  4. Find which equation to use
  5. Solve
  6. To get theta (\theta) by itself you have to use inverse sine (2nd function sine)
  7. Check which quadrants they are in to make sure that you get the correct angle.

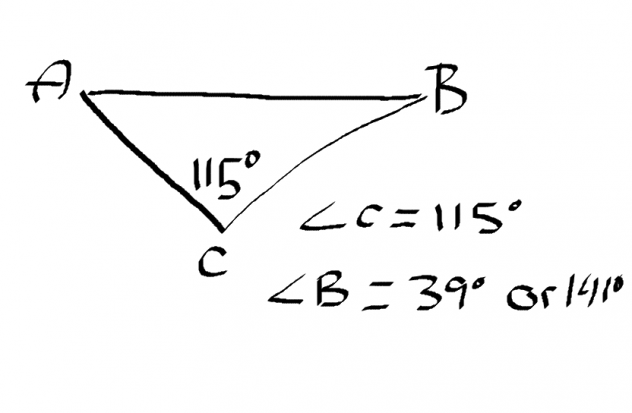
Example: Find Angle B

Step 1: Use the reciprocated version of the Sine Law \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}

Step 2: Find the given angles and side lengths

  • AB (c) = 10 cm
  • BC (a) = unknown
  • AC (b) = 7.0 cm
  • A = unknown
  • B = \theta
  • C = 150^o

Step 3: Fill in the Sine Law

  • \frac {Sin A}{a} = \frac {Sin B}{b} = \frac {Sin C}{c}
  • \frac {Sin A}{a} = \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}

Step 4: Find which equation to use..

\star I have enough information to use .

  • \frac {Sin B}{b} = \frac {Sin C}{c}
  • \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}

Step 5: Solve

  • \frac {Sin B}{7.0 cm} = \frac {Sin 115^o}{10 cm}
  • Sin B= \frac {Sin 115^o}{10 cm}\cdot 7.0 cm
  •  B= Sin^{-1}( \frac {Sin 115^o}{10 cm} \cdot 7.0 cm)
  • \angle B \doteq 39^o

Step 6: Check which quadrants they are in to make sure that you get the correct angle.

\star Using the cast rule

This means that Sin 39^o can be in either Quadrant 1 or 2 Because it will be positive where All and Sine is.

\star The reference angle in both Q1 and Q2 would be 39^o

\star The rotation angle in Q1 would be…

  • 0 + 39 = 39^o

\star The rotation angle in Q2 would be…

  • 180 – 39 = 141^o

\angle B can either be 39^o or 141^o

But since 141^o + 115^o = 256^o and exceeds the maximum amount a triangle can be with all three angles added together to make 180^o \angle B \neq 141^o

\therefore \angle B = 39^o and not 141^o

This is how you would use the Sine Law in Trigonometry

Grade 11, Math 11

Pre Calculus 11 Week 16: Multiplying and Dividing Rational Expressions

Leave a comment

During the Unit of Rational Expressions I have learned a few things like multiplying and dividing rational expressions. Compared to adding and subtracting these expressions it is a tad bit easier. I have learned to Just Do IT!

Steps When Multiplying Rational Expressions

  1. Simplify: Can do so by factoring to see if anything from the numerator and the denominator will cancel out.
  2. Multiply across: Just Do It!
  3. Simplify: By taking out a common factor if possible
  4. Variables: You can simplify variables too! If there is a x^2 on the denominator and a single x in the numerator we know that at least one pair can cancel out. The leftover variable will be left on the same side that it is on.
  5. State any Non Permissible values

Example 1: \frac{10x^2}{32x^3}\cdot\frac{4x}{22x^2}

Step 1: Simplify: Get the simplest form of each fraction by taking out a common factor.

In this case it is two

\star could be a different number for the two fractions, it’s not always the same.

  • \frac{10x^2}{32x^3}\cdot\frac{4x}{22x^2}
  • \frac{5x^2}{16x^3}\cdot\frac{2x}{11x^2}

You can also simplify the the variables

  • \frac{5x^2}{16x^3}\cdot\frac{2x^3}{11x^2}
  • \frac{5}{16x}\cdot\frac{2x}{11}

Step 2: Multiply across (Just Do It!)

  • \frac{5}{16x}\cdot\frac{2x}{11}
  • \frac{10x}{176x}

Step 3: Simplify by taking out common factors if possible

  • \frac{10x}{176x}
  • \frac{5x}{88x}

Step 4: Variables

  • \frac{5x}{88x}
  • \frac{5}{88}

Step 5: State any Non Permissible Values

x\neq 0

This is how you would multiply rational expressions

How to Divide Rational Expressions

Steps When Dividing Rational Expressions

Dividing rational expressions is very similar to that of multiplying. There is just one extra step. It is to reciprocate the fraction that is to right after the divide sign.

  1. Simplify: Can do so by factoring
  2. Reciprocate
  3. Cancel any pair terms
  4. Multiply across: Just Do It!
  5. Simplify: By taking out a common factor if possible
  6. Variables: You can simplify variables too! If there is a x^2 on the denominator and a single x in the numerator we know that at least one pair can cancel out. The left over variable will be left on the same side that it is on.
  7. State any Non Permissible values

Example 2: \frac{3x-27}{x^2 - 1}\cdot\frac{x^2 -7x - 8}{x^2 - 81}\div\frac{5x}{2x - 2}

Step 1: Simplify (factor)

  • \frac{3x-27}{x^2 - 1}\cdot\frac{x^2 -7x - 8}{x^2 - 81}\div\frac{5x}{2x - 2}
  • \frac{3(x-9)}{(x -1)(x +1)}\cdot\frac{(x-8)(x+1)}{(x-9)(x+9)}\div\frac{5x}{2(x - 1)}

Step 2: Reciprocate (this gets rid of the dividing sign and makes it a multiplying sign)

  • \frac{3(x-9)}{(x -1)(x +1)}\cdot\frac{(x-8)(x+1)}{(x-9)(x+9)}\div\frac{5x}{2(x-1)}
  • \frac{3(x-9)}{(x -1)(x +1)}\cdot\frac{(x-8)(x+1)}{(x-9)(x+9)}\cdot\frac{2(x - 1)}{5x}

Step 3: Cancel out any pair terms

  • \frac{3(x-9)}{(x -1)(x +1)}\cdot\frac{(x-8)(x+1)}{(x-9)(x+9)}\cdot\frac{2(x - 1)}{5x}
  • \frac{3}{1}\cdot\frac{(x-8)}{(x+9)}\cdot\frac{2}{5x}

Step 4: Multiply Across (Just Do It!)

  • \frac{3}{1}\cdot\frac{(x-8)}{(x+9)}\cdot\frac{2}{5x}
  • \frac {2\cdot 3\cdot (x-8)}{5x\cdot (x+9)}
  • \frac {6(x-8)}{5x(x+9)}

State the Non Permissible Values

x\neq { -9, -1, 0, 1, 9}

FINAL ANSWER: \frac {6(x-8)}{5x(x+9)}

This is how you would divide rational expressions.

Grade 11, Math 11

Pre Calculus 11 Week 15: Adding and Subtracting Rational Expressions With Binomial and Trinomial Denominators

Leave a comment

Image result for adding and subtracting rational expressions with binomial and trinomial denominators jokes

This week in Pre calculus 11 we learned how to add and subtract rational expressions that contained a binomial or trinomial denominator. These are quite ugly and difficult and require focus. I will show an example of each, and hopefully help you understand how to simplify these kinds of expressions.

Steps: Binomial Denominator 

  1. Simplify the Denominator if possible
  2. Find the Common Denominator
  3. Make Equivalent Fractions
  4. Add and or Subtract
  5. Simplify/Reduce
  6. State the Non-Permissible Values

Example: \frac{8}{6x+9} + \frac{3}{4x-4}

Step 1: Simplify the Denominator

  •  \frac{8}{6x+9} + \frac{3}{4x-4}
  • \frac{8}{3(2x+3)} + \frac{3}{4(x-1)}

Step 2: Find the Common Denominator

  • 3(2x+3)\cdot 4(x-1)
  • 12(2x+3)(x-1) = Common Denominator

Step 3: Make Equivalent Fractions

Multiply the denominator of one side to the other side (top and bottom) and then use the other denominator and multiply it to the other expression. Only multiply by what is need to get to the common denominator.

  • \frac{8}{3(2x+3}\cdot\frac{4(x-1)}{4(x-1)} + \frac{3}{4(x-1)}\cdot\frac{3(2x+3)}{3(2x+3)}
  • \frac{32(x-1)}{12(2x+3)(x-1)} + \frac{9(2x+3)}{12(2x+3)(x-1)}
  • \frac{32x-32}{12(2x+3)(x-1)} + \frac{18x+27}{12(2x+3)(x-1)}

Step 4: Add or Subtract                                                                                                    \star Make into one big fraction

  • \frac{32x-32 + 18x+27}{12(2x+3)(x-1)}

Step 5: Simplify/Reduce

  • \frac{32x - 32 + 18x + 27}{12( 2x + 3 )( x - 1)}
  • \frac{32x + 18x - 32 + 27}{12( 2x + 3 )( x - 1)}
  • \frac{50x - 5 }{12( 2x + 3 )( x - 1)}

\star Simplify the Numerator

  • \frac{50x - 5 }{12( 2x + 3 )( x - 1)}
  • \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}

Step 6: Non-Permissible Values

  • \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}
  • 12(2x+3)(x-1)
  • 2x + 3 = 0
  • 2x = -3
  • x = -\frac {3}{2}
  • x\neq -\frac {3}{2} , 1

FINAL ANSWER:  \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}

This is how you would simplify a rational expression with a binomial denominator

Steps: Trinomial Denominator 

  1. Simplify the Denominator if possible
  2. Find the Common Denominator
  3. Make Equivalent Fractions
  4. Add and or Subtract
  5. Simplify/Reduce
  6. State the Non-Permissible Values

Example: \frac{b}{b^2 + 10b + 24} + \frac{2b}{b^2 + 12b + 32}

Step 1: Simplify the Denominator

  • \frac{b}{b^2 + 10b + 24} + \frac{2b}{b^2 + 12b + 32}
  • \frac{b}{(b + 6)(b + 4)} + \frac{2b}{(b + 8)(b+4)}

Step 2: Find the Common Denominator

\star We know that we need a (b+8), a (b+4) and a (b+6) we don’t use the extra (b+4) because there is already one being used, we don’t want have any duplicates.

  • (b+8)(b+6)(b+4) = Common Denominator 

Step 3: Make Equivalent Fractions

Only multiply by what is needed to get to the common denominator 

  • \frac{b}{(b + 6)(b + 4)}\cdot\frac {b+8}{b+8} + \frac{2b}{(b + 8)(b + 4)}\cdot\frac {b+6}{b+6}
  • \frac{b(b+8)}{(b + 8)(b + 6)(b+4)} + \frac{2b(b+6)}{(b + 8)(b+6)(b+4)}
  • \frac{b^2+8b}{(b + 8)(b + 6)(b+4)} + \frac{2b^2+12b}{(b + 8)(b+6)(b+4)}

Step 4: Add or Subtract                                                                                                    \star Make into one big fraction

  • \frac{b^2+8b}{(b + 8)(b + 6)(b+4)} + \frac{2b^2+12b}{(b + 8)(b+6)(b+4)}
  • \frac{b^2+8b + 2b^2+12b}{(b + 8)(b+6)(b+4)}

Step 5: Simplify/Reduce

  • \frac{b^2+8b + 2b^2+12b}{(b + 8)(b+6)(b+4)}
  • \frac{b^2 + 2b^2+ 8b+ 12b}{(b + 8)(b+6)(b+4)}
  • \frac{3b^2+ 20b}{(b + 8)(b+6)(b+4)}

\star Simplify the Numerator

  • \frac{3b^2+ 20b}{(b + 8)(b+6)(b+4)}
  • \frac{b(3+ 20)}{(b + 8)(b+6)(b+4)}

Step 6: Non-Permissible Values

  • \frac{b(3+ 20)}{(b + 8)(b+6)(b+4)}
  • x\neq -8, -6, -4

This is how you would simplify Binomial and Trinomial Rational expressions when adding and or subtracting. I hope this blog post really helped you understand how to simplify these expressions. Feel free to look back at some of my other blog posts. They may help you with anything you are struggling with. Thanks 🙂

Below are two videos to help further understanding

here is a video that helped me understand how to add and subtract (binomial denominator) kinds of expressions.

And here is another video that helped me understand how to add and subtract rational expressions with a trinomial denominator (in the video the trinomial has already been factored).

 

Grade 11, Math 11

Pre-Calc 11: Week 14 Multiplying and Dividing Rational Expressions

Leave a comment

Last week in Pre-Calculus 11 we learned about multiplying and dividing rational expressions. A thing to remember about expressions is that it does not have an equal sign and you do not need to solve, you only need to simplify. I will be teaching you what non-permissible values are and how to determine what they are.

Non-permissible value :  Values that cause the fraction to have a denominator with a value of zero. (In math, we cannot divide by zero).

Here is an example of multiplying rational expressions

Steps: 

Step 1:  Simplify \frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}

Non permissible values: x\neq -3

  • \frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}
  • remove (x-3) from top and bottom because they cancel eachother out
  • then it becomes… \frac {3x}{2}\cdot\frac{8}{9x^2}

 

Step 2: Simplify by multiplying across (Just do it)

  • \frac {3x}{2}\cdot\frac{8}{9x^2}
  • \frac{24x}{18x^2}

Step 3: Take the highest common factor from both the numerator and the denominator.

In this case 6 is the highest number that goes into both.

  • \frac{24x}{18x^2}
  • \frac{4x}{18x^2}

Step 4: Notice that x is on the bottom and the top, if it has a pair it can cancel out. two x’s on the bottom one on the top. when they cancel out each other you will be left with only 1 on the bottom.

  • \frac{4x}{3x^2}
  • \frac{4}{3x}

Final Answer: \frac{4}{3x}

Dividing Rational Expressions 

There are many steps when dividing rational expressions

  1. Simplify the fraction: can factor or take out the common denominator.
  2. State the non permissible values.
  3. Reciprocate the second fraction and it will because a multiplication expression.
  4. State the restrictions again because there are new values in the denominator and could be non-permissible.
  5. Simplify (cancel out like terms that have a pair on the numerator and denominator.
  6. Multiply across (Just do it)
  7. Simplify again if possible.

Step 1: Simplify \frac{x+5}{x-4}\div\frac{x^2 - 25}{3x-12}

FACTOR:

  • \frac{x+5}{x-4}\div\frac{x^2 - 25}{3x-12}
  • \frac{x+5}{x-4}\div\frac{(x+5)(x-5)}{3(x-4)}

Step 2: Non-permissible values

  • x\neq 4

Step 3: Reciprocate

  • \frac{x+5}{x-4}\div\frac{(x+5)(x-5)}{3(x-4)}
  • \frac{x+5}{x-4}\cdot\frac{3(x-4)}{(x+5)(x-5)}

Step 4: Non-permissible values

  • x\neq 4
  • x\neq 5
  • x\neq -5

Step 5: Cross out like terms

  • \frac{x+5}{x-4}\cdot\frac{3(x-4)}{(x+5)(x-5)}
  • \frac{3}{(x-5)}

Step 6: Multiply across if possible

  • In this example it is not

Step 7: Simplify further if possible

  • In this example it is not

Final Answer:  \frac{3}{(x-5)}

 

This is how you Multiply and Divide Rational Expressions

 

 

Grade 11, Math 11

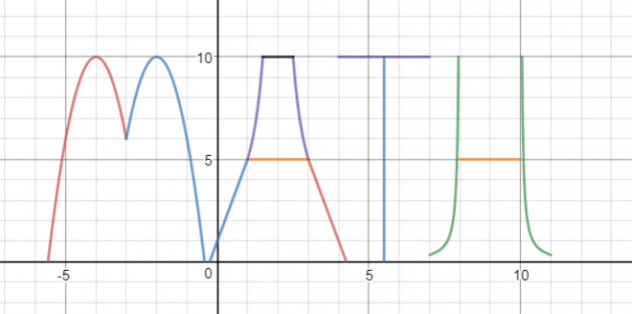
Pre Calculus: Week 13, Reciprocals of Linear Functions

Leave a comment

This week in Pre calc 11 we learned how to graph Reciprocals of Linear Functions.

Reciprocal functions are graphed with  y= \frac{1}{x}

How to graph a Reciprocals of Linear Functions

Step 1:  Graph the original Linear function

Step 2:  Find the Invariant Points (The Invariant Points are where the line meets  y= -1 and y=1. )

Step 3: Find the Asymptotes and draw in dashed lines for both. There is a vertical and horizontal one. This is an imaginary line in which a graph reciprocal function will approach but will never reach. The vertical asymptote for the line will be in the middle of the two Invariant Points. The Invariant Points are where the line meets  y= -1 and y=1.

Step 4:  Draw the hyperbola.

Let’s take -2x +5 and \frac{1}{-2x + 5} for example

  • The horizontal asymptote is y=0
  • The vertical asymptotes is x = 2.5
    • A thing to notice when trying to find the vertical asymptote is that it is where the original line’s x axis is.
    • It is also in the middle of the two invariant points

The invariant points would be (2, 1) and (3, -1)

Things you will have to define for  \frac{1}{-2x + 5}

  • x intercept : none the reciprocated function does not cross the x axis because there is a horizontal asymptote
  • y axis: y= 0.2
  • Domain: XER,  x\neq 2.5
  • Range: YER, y\neq 0
  • Asymptotes:
    • horizontal : y = 0
    • vertical : x = 2.5

This is how you would graph Reciprocals of Linear Functions.

 

Grade 11, Math 11

Pre Calculus Week 12:

Leave a comment

This week in Pre-Calc 11 we started a new unit; Absolute Values and Reciprocal Functions. We continued off of the linear and quadratic functions we learned about, and how to graph these new kinds of functions. I will also show you how to right piecewise notation.

Reminder

linear function: y=mx+b

Quadratic: y= a(x-p)^2 + q

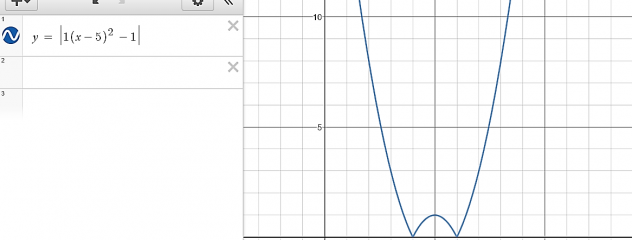
|Absolute value signs| : The distance away from zero, makes every number in between these lines positive.

When an absolute value symbol is added into an equation, it will force any part of the line or parabola that is in the bottom (negative) of the graph to flip and become positive. When this happens the point at where the line will have an immediate turning point also known as the point of inflection or as the critical point. This point usually has an x value and a y value of 0.

A few thing you will need to identify are:

  1. Point of Inflection (x intercept)
  2. y intercept
  3. Damain
  4. Range

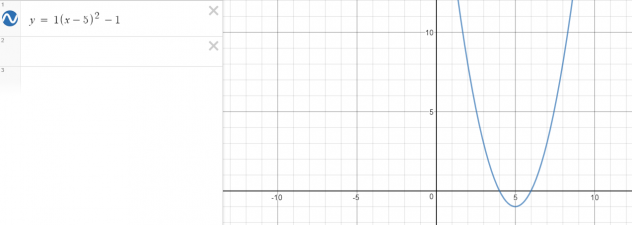
Example: y= 4x +6 and y = |4x+6|

y=4x+6

Will turn into… when absolute value signs are added

Identify:

point of inflection:( -1.5, 0 )

y intercept: ( 0, 6 )

Domain: XER (because the graph goes on forever in each direction)

Range: y\underline{>} 0

Piecewise Notation

This a way to describe a function, and it has two parts.

  1. The first part, we write the original equation and when it is positive

 

 

 

 

 

This would be how to describe the positive part of the line

 

2.  The second part of the piecewise notation would be described by placing brackets around the equation and a negative in front to flip it to become positive 

The restriction helps to tell where the description occurs

3.  Now combine the two parts like…

This would be the complete way to write piecewise notation, and how to fully describe the function

Parabola

This would be very similar to a parabola

example: y = |1(x-5)^2 -1|

Would turn into…

 

Piecewise notation

The first part of the piecewise notation explains that any x value smaller than 4 will be positive and any number larger than 6 will also be positive.

The second part of the piecewise notation describes where the parabola would be negative, but it has been placed with the negative sign so it makes whatever is in the negative side positive. So any points between 4 and 6 would be negative, but the absolute value signs have made it.

positive.

 

This is how you would write piecewise notation as well as what a linear and quadratic function would look like on graphs when introduced with absolute value signs.

Grade 11, Math 11

Pre Calculus 11 Week 11: Graphing Linear Inequalities in Two Variables

Leave a comment

This week in week 11 we started Graphing Inequalities. The majority of this is related to our graphing from last year in grade 10 math.

Linear graphs are known as straight line graphs with the equation of y=mx +b.

m is the slope ( \frac{rise}{run} )                                                                                                            b is the y intercept

For example: y =\frac{1}{2}x + 6 on a graph looks like:

Now when graphing inequalities you have to find a sign that will have a true statement after you have chosen a point on the graph to substitute x and y.

\star Note that > and < are broken lines on the graph and \underline{<} and \underline{>} are solid lines like the above graph ( because it is equal to so it includes the line)

  • 0 < \frac{1}{2}x + 6 (greater than zero)
  • 0 \underline{<} \frac{1}{2}x + 6 (greater or equal to zero)
  • 0 > \frac {1}{2}x + 6 (less than zero)
  • 0 \underline{>} \frac {1}{2}x + 6 (less than or equal to zero)

Now to graph the inequality you have to choose a point on the graph that makes the expression true for example:

y < \frac{1}{2}x + 6

\star to make things easy use (0,0) as the point

  •  y < \frac{1}{2}x + 6
  •  0 < \frac{1}{2}(0) + 6
  • 0 < 0 + 6
  • 0 < 6

This statement is true because 0 is smaller than 6. This means that the side that has the coordinate of (0,0) will be shaded in. This will also have a broken line because it is not equal to.

Now when we change the sign to greater to (>) it will flip because 0 would not be greater than 6

 

  • y > \frac{1}{2}x + 6
  •  0 > \frac{1}{2}(0) + 6
  • 0 > 0 + 6
  • 0 > 6
  • FALSE STATEMENT

If the sign was \underline {>} or \underline {<} the line would be solid.

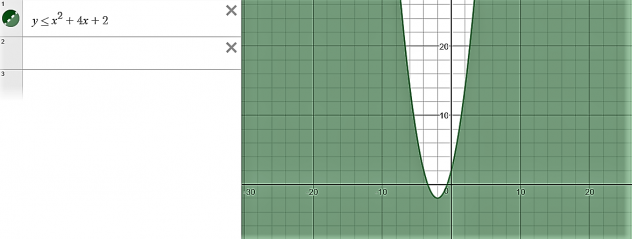
You can also graph a parabola

example: y = x^2 + 4x + 2

Step one: Graph the parabola by putting it into standard form.

  • y = x^2 + 4x + 2
  • y =\underbrace{x^2 + 4x + 4} - 4 + 2
  • y = (x + 2)^2 -4 + 2
  • y = (x + 2)^2 -2

Graph it from here.

Step two: chose a point on the graph and make a true statement.

  • y \underline{<} x^2+4x+2
  • 0 \underline{<} 0 + 0 +2
  • 0 \underline{<} 2
  • TRUE STATEMENT, 0 is smaller than two

The side with (0,0) as a coordinate will be shaded in and the line will be solid because it is equal to.

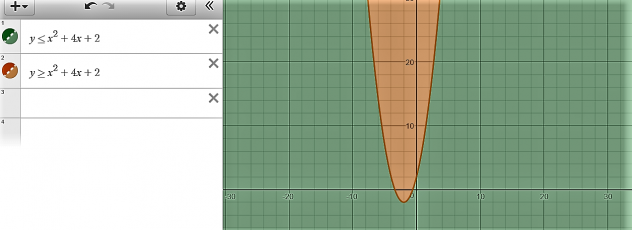
Now if the sign was change the inside of the parabola would be shaded in.

This is how to graph inequalities with linear equations as well as quadratic equations.

Grade 11, Math 11

Pre Calculus 11 Week 10: Reviewing Factoring with Substitution

Leave a comment

Last week in Pre Calculus 11 we mostly reviewed for our midterm exam. As I was studying I came across a few things that I totally forgot about. Things that would help make my math life easier, like how to use substitution when factoring. This is helpful because it is simple, faster, and not as messy as factoring without this trick. I will quickly review how to do this.

Example: 3(2x-1)^2 + 14(2x-1) + 8

Step 1: Substitute (2x-1) with a variable.

\star Notice that there are two (2x-1), therefore you can use the same variable for both terms.

  • 3a^2 + 14a + 8

Step 2: Factor3a^2 + 14a + 8

  • (3a + 2) (a + 4)

Step 3: Substitute (2x – 1) back into the factored form to replace the variable a.

  • (3a + 2) (a + 4)
  • (3(2x -1) + 2) ((2x-1)+ 4

Step 4: Distribute

  • (3(2x -1) + 2) ((2x-1)+ 4
  • (6x-3 +2)(2x-1+4)

Step 5: Simplify

  • (6x-3 +2)(2x-1+4)
  • (6x-1)(2x+3)

FINAL ANSWER

(6x-1)(2x+3)

To find the solutions make each factor equal to zero and solve for x:

6x-1=0 –> 6x=1 –> x=\frac{1}{6}

2x + 3=0 –>2x=-3 –> x =- \frac{3}{2}

This is how to use substitution while factoring. This is a very helpful and quick way to factor difficult looking equations.