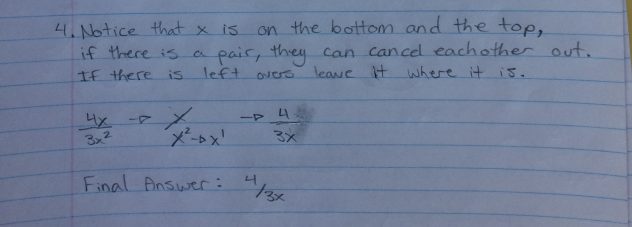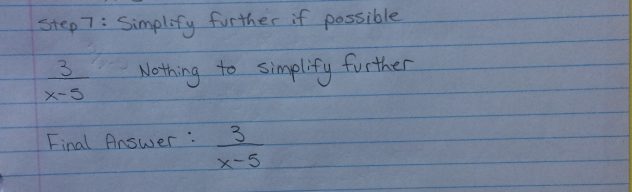Monthly Archives: May 2018

Grade 11, Socials 11

Socials 11: Defining Poverty

Leave a comment
  1. In your own words, explain the problems with measuring poverty (standard of living, absolute vs relative, HDI)
  • There are many problems when trying to define poverty. Many countries live in different situations, for example a less developed country may seem poor to a more developed country. This is called standard of living. Some countries like Canada have a higher standard of living than others. When comparing absolute poverty vs. relative poverty on one country compared to another it can be different. The needs of a person in a developed country is higher for example the low standard of living for a higher developed country could very well be the higher standard of living for a less developed country. Absolute poverty is when you do not have enough support or money to afford the essentials in life, and relative poverty is being able to afford your basic needs. Canada’s absolute poverty could be another countries relative poverty. This is why it is difficult to determine if a country is poor while being compared to another country.
  1. What do you think is the best way to measure poverty in Canada and the world.
  • I think the best way to measure poverty in Canada and the world is to use the Human Development Index. I think gathering number relative to that countries standard of living adding it together and then comparing it might help even out and help determine if a country is in actual poverty or not. Basic Human Needs, which includes medical care, sanitation, and shelter foundations of wellbeing, which covers education, access to technology, and life expectancy and opportunity, which looks at personal rights, freedom of choice, and general tolerance is a way that could help determine if a country is poor when all these factors are added up and compared.
  • I think that this would be better than just comparing the economic growth of a country because it adds more factors into effect and will be more accurate and comparable.
Grade 11, Math 11

Pre Calculus 11 Week 15: Adding and Subtracting Rational Expressions With Binomial and Trinomial Denominators

Leave a comment

Image result for adding and subtracting rational expressions with binomial and trinomial denominators jokes

This week in Pre calculus 11 we learned how to add and subtract rational expressions that contained a binomial or trinomial denominator. These are quite ugly and difficult and require focus. I will show an example of each, and hopefully help you understand how to simplify these kinds of expressions.

Steps: Binomial Denominator 

  1. Simplify the Denominator if possible
  2. Find the Common Denominator
  3. Make Equivalent Fractions
  4. Add and or Subtract
  5. Simplify/Reduce
  6. State the Non-Permissible Values

Example: \frac{8}{6x+9} + \frac{3}{4x-4}

Step 1: Simplify the Denominator

  •  \frac{8}{6x+9} + \frac{3}{4x-4}
  • \frac{8}{3(2x+3)} + \frac{3}{4(x-1)}

Step 2: Find the Common Denominator

  • 3(2x+3)\cdot 4(x-1)
  • 12(2x+3)(x-1) = Common Denominator

Step 3: Make Equivalent Fractions

Multiply the denominator of one side to the other side (top and bottom) and then use the other denominator and multiply it to the other expression. Only multiply by what is need to get to the common denominator.

  • \frac{8}{3(2x+3}\cdot\frac{4(x-1)}{4(x-1)} + \frac{3}{4(x-1)}\cdot\frac{3(2x+3)}{3(2x+3)}
  • \frac{32(x-1)}{12(2x+3)(x-1)} + \frac{9(2x+3)}{12(2x+3)(x-1)}
  • \frac{32x-32}{12(2x+3)(x-1)} + \frac{18x+27}{12(2x+3)(x-1)}

Step 4: Add or Subtract                                                                                                    \star Make into one big fraction

  • \frac{32x-32 + 18x+27}{12(2x+3)(x-1)}

Step 5: Simplify/Reduce

  • \frac{32x - 32 + 18x + 27}{12( 2x + 3 )( x - 1)}
  • \frac{32x + 18x - 32 + 27}{12( 2x + 3 )( x - 1)}
  • \frac{50x - 5 }{12( 2x + 3 )( x - 1)}

\star Simplify the Numerator

  • \frac{50x - 5 }{12( 2x + 3 )( x - 1)}
  • \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}

Step 6: Non-Permissible Values

  • \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}
  • 12(2x+3)(x-1)
  • 2x + 3 = 0
  • 2x = -3
  • x = -\frac {3}{2}
  • x\neq -\frac {3}{2} , 1

FINAL ANSWER:  \frac{5(10x - 1) }{12( 2x + 3 )( x - 1)}

This is how you would simplify a rational expression with a binomial denominator

Steps: Trinomial Denominator 

  1. Simplify the Denominator if possible
  2. Find the Common Denominator
  3. Make Equivalent Fractions
  4. Add and or Subtract
  5. Simplify/Reduce
  6. State the Non-Permissible Values

Example: \frac{b}{b^2 + 10b + 24} + \frac{2b}{b^2 + 12b + 32}

Step 1: Simplify the Denominator

  • \frac{b}{b^2 + 10b + 24} + \frac{2b}{b^2 + 12b + 32}
  • \frac{b}{(b + 6)(b + 4)} + \frac{2b}{(b + 8)(b+4)}

Step 2: Find the Common Denominator

\star We know that we need a (b+8), a (b+4) and a (b+6) we don’t use the extra (b+4) because there is already one being used, we don’t want have any duplicates.

  • (b+8)(b+6)(b+4) = Common Denominator 

Step 3: Make Equivalent Fractions

Only multiply by what is needed to get to the common denominator 

  • \frac{b}{(b + 6)(b + 4)}\cdot\frac {b+8}{b+8} + \frac{2b}{(b + 8)(b + 4)}\cdot\frac {b+6}{b+6}
  • \frac{b(b+8)}{(b + 8)(b + 6)(b+4)} + \frac{2b(b+6)}{(b + 8)(b+6)(b+4)}
  • \frac{b^2+8b}{(b + 8)(b + 6)(b+4)} + \frac{2b^2+12b}{(b + 8)(b+6)(b+4)}

Step 4: Add or Subtract                                                                                                    \star Make into one big fraction

  • \frac{b^2+8b}{(b + 8)(b + 6)(b+4)} + \frac{2b^2+12b}{(b + 8)(b+6)(b+4)}
  • \frac{b^2+8b + 2b^2+12b}{(b + 8)(b+6)(b+4)}

Step 5: Simplify/Reduce

  • \frac{b^2+8b + 2b^2+12b}{(b + 8)(b+6)(b+4)}
  • \frac{b^2 + 2b^2+ 8b+ 12b}{(b + 8)(b+6)(b+4)}
  • \frac{3b^2+ 20b}{(b + 8)(b+6)(b+4)}

\star Simplify the Numerator

  • \frac{3b^2+ 20b}{(b + 8)(b+6)(b+4)}
  • \frac{b(3+ 20)}{(b + 8)(b+6)(b+4)}

Step 6: Non-Permissible Values

  • \frac{b(3+ 20)}{(b + 8)(b+6)(b+4)}
  • x\neq -8, -6, -4

This is how you would simplify Binomial and Trinomial Rational expressions when adding and or subtracting. I hope this blog post really helped you understand how to simplify these expressions. Feel free to look back at some of my other blog posts. They may help you with anything you are struggling with. Thanks 🙂

Below are two videos to help further understanding

here is a video that helped me understand how to add and subtract (binomial denominator) kinds of expressions.

And here is another video that helped me understand how to add and subtract rational expressions with a trinomial denominator (in the video the trinomial has already been factored).

 

Grade 11, Math 11

Pre-Calc 11: Week 14 Multiplying and Dividing Rational Expressions

Leave a comment

Last week in Pre-Calculus 11 we learned about multiplying and dividing rational expressions. A thing to remember about expressions is that it does not have an equal sign and you do not need to solve, you only need to simplify. I will be teaching you what non-permissible values are and how to determine what they are.

Non-permissible value :  Values that cause the fraction to have a denominator with a value of zero. (In math, we cannot divide by zero).

Here is an example of multiplying rational expressions

Steps: 

Step 1:  Simplify \frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}

Non permissible values: x\neq -3

  • \frac{3x}{2(x-3)}\cdot\frac{8(x-3)}{9x^2}
  • remove (x-3) from top and bottom because they cancel eachother out
  • then it becomes… \frac {3x}{2}\cdot\frac{8}{9x^2}

 

Step 2: Simplify by multiplying across (Just do it)

  • \frac {3x}{2}\cdot\frac{8}{9x^2}
  • \frac{24x}{18x^2}

Step 3: Take the highest common factor from both the numerator and the denominator.

In this case 6 is the highest number that goes into both.

  • \frac{24x}{18x^2}
  • \frac{4x}{18x^2}

Step 4: Notice that x is on the bottom and the top, if it has a pair it can cancel out. two x’s on the bottom one on the top. when they cancel out each other you will be left with only 1 on the bottom.

  • \frac{4x}{3x^2}
  • \frac{4}{3x}

Final Answer: \frac{4}{3x}

Dividing Rational Expressions 

There are many steps when dividing rational expressions

  1. Simplify the fraction: can factor or take out the common denominator.
  2. State the non permissible values.
  3. Reciprocate the second fraction and it will because a multiplication expression.
  4. State the restrictions again because there are new values in the denominator and could be non-permissible.
  5. Simplify (cancel out like terms that have a pair on the numerator and denominator.
  6. Multiply across (Just do it)
  7. Simplify again if possible.

Step 1: Simplify \frac{x+5}{x-4}\div\frac{x^2 - 25}{3x-12}

FACTOR:

  • \frac{x+5}{x-4}\div\frac{x^2 - 25}{3x-12}
  • \frac{x+5}{x-4}\div\frac{(x+5)(x-5)}{3(x-4)}

Step 2: Non-permissible values

  • x\neq 4

Step 3: Reciprocate

  • \frac{x+5}{x-4}\div\frac{(x+5)(x-5)}{3(x-4)}
  • \frac{x+5}{x-4}\cdot\frac{3(x-4)}{(x+5)(x-5)}

Step 4: Non-permissible values

  • x\neq 4
  • x\neq 5
  • x\neq -5

Step 5: Cross out like terms

  • \frac{x+5}{x-4}\cdot\frac{3(x-4)}{(x+5)(x-5)}
  • \frac{3}{(x-5)}

Step 6: Multiply across if possible

  • In this example it is not

Step 7: Simplify further if possible

  • In this example it is not

Final Answer:  \frac{3}{(x-5)}

 

This is how you Multiply and Divide Rational Expressions

 

 

Grade 11, Socials 11

WW1: The Chain of Friendship

1 Comment

  • A: Serbia
  • B: Austria
  • C: Russia
  • D: Germany
  • E: France
  • F: Britain

Theme: Alliances

  • The people circled in blue (Serbia, Russia, France and Britain) have an alliance.
  • The people circled in yellow have an alliance as well (Austria and Germany)

Explain the History:

  • Austria blamed Serbia for the assassination of Franz Ferdinand.
  • Russia is shown to side with Serbia and goes against Austria.
  • Germany is in alliance with Austria so is opposed to Russia and Serbia.
  • France and Britain side with Russia because of the Triple Entente.

Explain the History of Serbia:

  • Serbia is shown as the little guy because they don’t stand against Austria until Germany supports them. Austria blamed Serbia for the assassination of  Franz Ferdinand (Archduke).

Theme:

  • Imperialism

Explain the History:

  • France and Britain attacked Germany because Germany violated the neutrality of Belgium in order to attack France, Britain then declared war on Germany to protect its ally Russia.

Explain the History:

  • Imperialism: because the Great Powers were struggling to expand their colonies around the world, they also fought over limited resources in Europe. Of particular were the Balkans, a culture promoted around the Adriatic Sea in southeastern Europe. Russia wanted to control this area and so did the Great  Powers who wanted to expand their colonies. 

Sequence of Events:

  1. Austria’s leader Archduke Ferdinand goes to Bosnia he is assassinated and Austria blames Serbia for this
  2. Serbia refuses to admit/give in to this accusation, Germany supports Austria and says that it will help with any military actions that Austria does.
  3. Austria goes at war with Serbia, because Serbia doesn’t accept the ultimatum, and Russia helps Serbia fight.
  4. Austria-Hungary and Germany tell Russia to not fight, Russia doesn’t listen
  5. Germany helps Austria and declares war on Russia and France
  6. Britain goes to help it’s allies Russia and France
  7. Canada as part of the British Empire is involved now too
  • A: I think that this could be in Russia’s perspective or may the other from the Triple Entente. Everyone else seems too weak and or too violent. The triple Entente were more of the good guys and would stand up for what they believe in and because they had more support from other countries. This makes them not afraid to say something.
  • B: The first country is depicted as a child because it is a metaphor that Serbia has little power and is no match to the other countries.
  • C: I think that the Title is ironic because they aren’t really friends, they are just allies who are protecting themselves. Each country had their own selfish purpose for getting involved. Germany wanted to build its empire and prove its army. France and Britain have have a grudge on  Germany and aren’t really that concerned for Serbia. As for Russia, their ideologies opposed Austria-Hungary’s seizure of Sarajevo and did not want Austria-Hungary expanding into the Balkans. So Russia agreed to join Serbia if Austria-Hungary attacked. They did not do all these things just to help their “friends” they did this because they were selfish.
Grade 11, Math 11

Pre Calculus: Week 13, Reciprocals of Linear Functions

Leave a comment

This week in Pre calc 11 we learned how to graph Reciprocals of Linear Functions.

Reciprocal functions are graphed with  y= \frac{1}{x}

How to graph a Reciprocals of Linear Functions

Step 1:  Graph the original Linear function

Step 2:  Find the Invariant Points (The Invariant Points are where the line meets  y= -1 and y=1. )

Step 3: Find the Asymptotes and draw in dashed lines for both. There is a vertical and horizontal one. This is an imaginary line in which a graph reciprocal function will approach but will never reach. The vertical asymptote for the line will be in the middle of the two Invariant Points. The Invariant Points are where the line meets  y= -1 and y=1.

Step 4:  Draw the hyperbola.

Let’s take -2x +5 and \frac{1}{-2x + 5} for example

  • The horizontal asymptote is y=0
  • The vertical asymptotes is x = 2.5
    • A thing to notice when trying to find the vertical asymptote is that it is where the original line’s x axis is.
    • It is also in the middle of the two invariant points

The invariant points would be (2, 1) and (3, -1)

Things you will have to define for  \frac{1}{-2x + 5}

  • x intercept : none the reciprocated function does not cross the x axis because there is a horizontal asymptote
  • y axis: y= 0.2
  • Domain: XER,  x\neq 2.5
  • Range: YER, y\neq 0
  • Asymptotes:
    • horizontal : y = 0
    • vertical : x = 2.5

This is how you would graph Reciprocals of Linear Functions.

 

Socials 11

Conserving Water

1 Comment

Why is it important to conserve water in Canada?

It is important to save water in Canada because the majority of our land is farmland. We need to cut down on our water usage so we don’t run out of it and lower our other resources. Another reason why we should conserve water is so we don’t create more waste water and have to use more energy to clean it, as well as keeping our environment clean because our environment can only take so much and if we continue to pollute it then we are hurting the environment and hurting ourselves.

Something I already do to save water is turn the tap off when i brush my teeth. A new way for me to save water that i am going to implement into my life is take shorter showers as well as wash my face in the shower instead of doing it in the sink with the water running.

 

Grade 11, Math 11

Pre Calculus Week 12:

Leave a comment

This week in Pre-Calc 11 we started a new unit; Absolute Values and Reciprocal Functions. We continued off of the linear and quadratic functions we learned about, and how to graph these new kinds of functions. I will also show you how to right piecewise notation.

Reminder

linear function: y=mx+b

Quadratic: 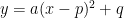y= a(x-p)^2 + q

|Absolute value signs| : The distance away from zero, makes every number in between these lines positive.

When an absolute value symbol is added into an equation, it will force any part of the line or parabola that is in the bottom (negative) of the graph to flip and become positive. When this happens the point at where the line will have an immediate turning point also known as the point of inflection or as the critical point. This point usually has an x value and a y value of 0.

A few thing you will need to identify are:

  1. Point of Inflection (x intercept)
  2. y intercept
  3. Damain
  4. Range

Example: y= 4x +6 and y = |4x+6|

y=4x+6

Will turn into… when absolute value signs are added

Identify:

point of inflection:( -1.5, 0 )

y intercept: ( 0, 6 )

Domain: XER (because the graph goes on forever in each direction)

Range: y\underline{>} 0

Piecewise Notation

This a way to describe a function, and it has two parts.

  1. The first part, we write the original equation and when it is positive

 

 

 

 

 

This would be how to describe the positive part of the line

 

2.  The second part of the piecewise notation would be described by placing brackets around the equation and a negative in front to flip it to become positive 

The restriction helps to tell where the description occurs

3.  Now combine the two parts like…

This would be the complete way to write piecewise notation, and how to fully describe the function

Parabola

This would be very similar to a parabola

example: y = |1(x-5)^2 -1|

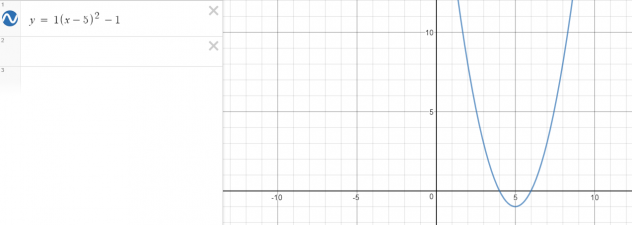
Would turn into…

 

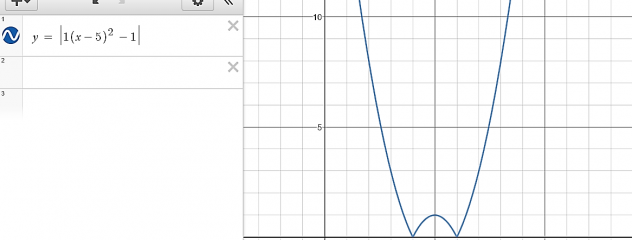
Piecewise notation

The first part of the piecewise notation explains that any x value smaller than 4 will be positive and any number larger than 6 will also be positive.

The second part of the piecewise notation describes where the parabola would be negative, but it has been placed with the negative sign so it makes whatever is in the negative side positive. So any points between 4 and 6 would be negative, but the absolute value signs have made it.

positive.

 

This is how you would write piecewise notation as well as what a linear and quadratic function would look like on graphs when introduced with absolute value signs.

Socials 11

Poverty Life Cycles

1 Comment

POVERTY CYCLE OF HIV

  1. Baby Born with HIV
  2. Mother dies giving birth
  3. Child is unable to receive treatment
  4. Child cannot attend school because child has to work to get treatment 
  5. Child will start a family at a young age because no education

Solution: to have charities that help fund countries with medical care for free so families can save money and increase survival rates and allow kids to focus on education and be able to obtain a good job in the future.

WOMENS EQUALITY POVERY CYCLE

  1. Woman born into inequality
  2. Not treated fairly
  3. Woman gets taken advantage of at a young age (Rape) gets pregnant
  4. Woman cannot get education
  5. Woman only works at home

Solution: Allow girls to get education and make the education more generalized for everyone about poverty and health as well as normal school subjects. This will allow both genders to be aware of the possibilities of having children at an early age and will allow for woman to put off children until after education, which will allow for the woman to build a family without getting stuck in poverty.

CHILD BORN INTO POVERTY

  1. Child born into poverty
  2. Family cannot afford food
  3. Child needs to work for family
  4. Child receives no education
  5. Child has kids at a young age sue to lack of education/ family planning

Solutions: Make laws that protect child workers  and force companies to provide education for student workers for them to receive and education and help their development instead of damaging it.