This week in Pre Calculus 11, we learned what an absolute value of a real number was and how to simplify radical expressions.
Absolute Value of a Real Number : The principal square root of a square number.
SOLUTION: The absolute value of a negative number is the opposite number, and the absolute value of a positive number and 0 are the same.
ex/ |-99| = 99 | 12 | = 12
This is because distance is always positive.
The long lines act as brackets but are not and it represents absolute value.
- ex 1/ 4 |15-20|
- 4 |-5|
- 4 (5)
- = 20
- ex 2/ |6 +(-10)| -|5-7|
- |6-10| – | -2|
- |-4| – |2|
- 4 – 2
- = 2
Here is a video that really helped me learn and understand a little bit more about absolute value.
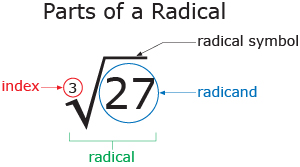
Radical Expressions
we also briefly reviewed radical expressions
Here a link to another post for radical expressions : http://myriverside.sd43.bc.ca/jessicap2015/2017/02/11/math-10-week-2/
ex/ = 5 and
=
Now to build off of radical expressions we are adding variables.
Solving
Step 1: Find perfect squares.
Step 2: Take them out / simplify
Step 3: Do the same with the variables (treat them like numbers)
ex/
- ex/
This is how to work with variables in Radical Expressions