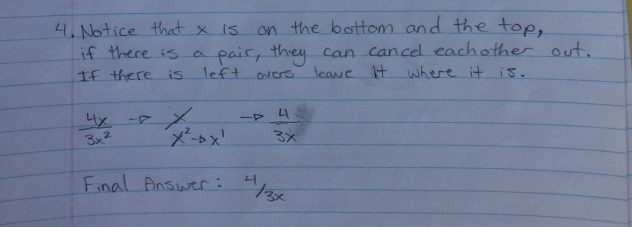This week in Pre-Calc 11 we started a new unit; Absolute Values and Reciprocal Functions. We continued off of the linear and quadratic functions we learned about, and how to graph these new kinds of functions. I will also show you how to right piecewise notation.
Reminder
linear function: y=mx+b
Quadratic: 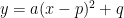
|Absolute value signs| : The distance away from zero, makes every number in between these lines positive.
When an absolute value symbol is added into an equation, it will force any part of the line or parabola that is in the bottom (negative) of the graph to flip and become positive. When this happens the point at where the line will have an immediate turning point also known as the point of inflection or as the critical point. This point usually has an x value and a y value of 0.
A few thing you will need to identify are:
- Point of Inflection (x intercept)
- y intercept
- Damain
- Range
Example: y= 4x +6 and y = |4x+6|
y=4x+6

Will turn into… when absolute value signs are added
Identify:
point of inflection:( -1.5, 0 )
y intercept: ( 0, 6 )
Domain: XER (because the graph goes on forever in each direction)
Range: 
Piecewise Notation
This a way to describe a function, and it has two parts.
- The first part, we write the original equation and when it is positive


This would be how to describe the positive part of the line
2. The second part of the piecewise notation would be described by placing brackets around the equation and a negative in front to flip it to become positive 
The restriction helps to tell where the description occurs
3. Now combine the two parts like…

This would be the complete way to write piecewise notation, and how to fully describe the function
Parabola
This would be very similar to a parabola
example: 
Would turn into…
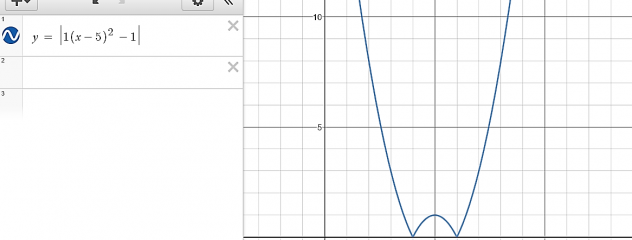
Piecewise notation

The first part of the piecewise notation explains that any x value smaller than 4 will be positive and any number larger than 6 will also be positive.
The second part of the piecewise notation describes where the parabola would be negative, but it has been placed with the negative sign so it makes whatever is in the negative side positive. So any points between 4 and 6 would be negative, but the absolute value signs have made it.
positive.
This is how you would write piecewise notation as well as what a linear and quadratic function would look like on graphs when introduced with absolute value signs.