This week in Math 11 we learned about sign charts which help us find our roots by factoring then once we find our roots we use a number line and our roots to figure out different signs of our parabola and to know which numbers we can use to replace the variable and solve to make the equation true.
Example: 4x 2
- This is our equation so, the first thing we do is to factor and find our roots.
4x 2
4x
0
0
0
0 2(x – 3)(x + 1)
- Now that we know our roots we can use a sign chart to figure out information about which numbers make the equation true.
- We can find out whether our parabola opens up or down.
– – 0 +
(x – 3): x = 3 -1 3
- For this one our zero would be 3 because our”x” is equal to zero
- on a number line everything to the right of “0” is positive and everything to the left is negative.
– 0 + +
(x + 1): x = -1 -1 3
- For this one our zero would be -1 because our “x” is equal to zero
Now if we put these together we can find out to number to make our equation true.
– – 0 +
(x – 3): x = 3 -1 3
– 0 + +
(x + 1): x = -1 -1 3
- Now we look at each column of the signs and multiply them
– – 0 +
(x – 3): x = 3 -1 3
– 0 + +
(x + 1): x = -1 -1 3
(-)(-) = + (-)(+) = – (+)(+) = +
Positive(+) Negative(-) Positive(+)
Now if we look back at our original equation: 4x 2
- we see that 4x is less than or equal to $ 2
- so to figure out which section makes the equation true we would get a number from each section and plug it in to our original equation to see whether it is true or false
– – 0 +
(x – 3): x = 3 -1 3
– 0 + +
(x + 1): x = -1 -1 3
(-)(-) = + (-)(+) = – (+)(+) = +
Positive(+) Negative(-) Positive(+)
Section 1: use -2 Section 2: use 0 Section 3: use 4
- NOTE: Always use “0” as a test number if possible.
Section 1: use -2
4x 2
4(-2) 2
-8 2 (4 – 3)
-8 2 (1)
-8 2
True
- -8 is less than 2
Section 2: use 0
4x 2
4(0) 2
0 2 (0 – 3)
0 2 (-3)
0 -6
False
- 0 is NOT less than -6
Section 3: use 4
4x 2
4(4) 2
16 2
16 2
16 26
True
- 16 is less than 26
Now that we know which ones are true and which ones are false we can write our answer.
- Because our sections that are true are the outer sections we write our answers for “x” separately.
- if the true section was the middle section and the outer sections were false we would combine our answer for “x”.
- In our original equation we used the “equal to” sign as well , so we would use this for our answer as well.
Answer:
x -1
and
x 3

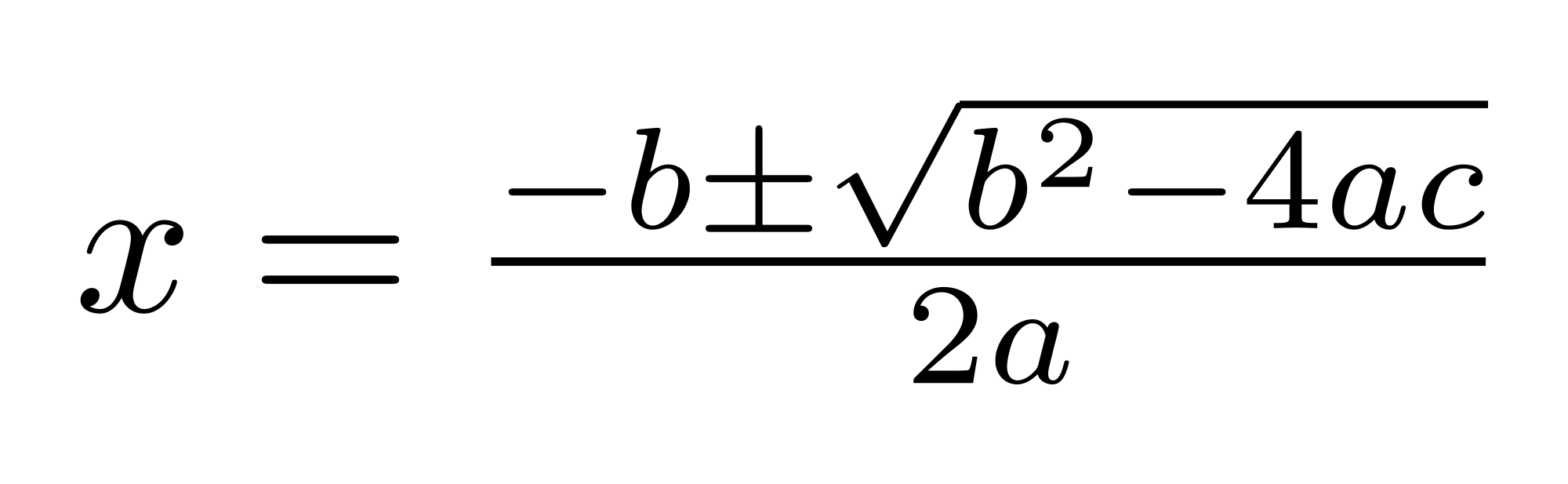
 Area of this square = 40
Area of this square = 40 
