this week in math 10 I wasn’t there for any of the week because I was sick but I learned about elimination and substitution for solving solutions by finding x and y.
With finding the x and y coordinates we learned how to graph them even by just the equation.
We had to use previous knowledge to help us change the equations from general form to slope y intercept form for letting us solve the equations
In week 15 in math 10 we learned how to find the slops of a graph. the slope in this is 2/4 because it rises by 2 and runs by 4. And this slope is a positive slope because its going up. If you do not have an exact rise and run you look for the “nice points” and use those to direct you to find your rise and run.
the slope in this is 2/4 because it rises by 2 and runs by 4. And this slope is a positive slope because its going up. If you do not have an exact rise and run you look for the “nice points” and use those to direct you to find your rise and run.
In week 14 of math 10 we learned how to tell the difference between a function or a relation just by looking at a graph, mapping diagram or a table chart.
graphing: If there are dots that have the filled in circle that are found vertically on the sae x value then that is a relation, if there are two lines found vertically above each other than that is a relation as well.
mapping diagram: If your X values are the same then that is a relation, if they are all different that is a function, the only way for X to have the same values as each other is if the Y values are the same for both.
table chart: If your X values are the same then that is a relation, if they are all different that is a function, the only way for X to have the same values as each other is if the Y values are the same for both.

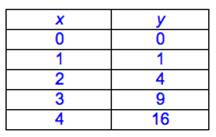

In week 13 in math 10 we learned how to tell the difference between a relation and a function and what they are, we learner what and input and output were, what a independent and dependant variable is, we learned how they are graphed and 5 ways to express them which can be by a table of value, ordered pairs, graphing, an equation and a mapping graph.
Independent, input, x and range all mean the same thing.
Dependant, output, y and domain all mean the same thing.
Relation- numbers that have common multiple, numbers may varie in similarity.
Function- numbers that have no common multiples and they are singular meaning no number will be the same.

In week 11 of math 10 we learned how to factor perfect trinomials and how to use CDPEU (common, difference in squares, pattern, easy, ugly) to make it easier to factor. When you factor the binomials they will be identical and then you have to expand and simplify the terms. The first term and the last term will be squared numbers, the middle term will equal the square root of the of the last term multiplied by the square root of the middle term.

In week 10 of math 10 I learned how to expand and how to use factorization on polynomials. At first the methods we were using didn’t make complet sense to me but now they do and the questions weren’t too hard I understood most of them but It just took some help on the ones I didn’t understand. For most of the question you had to find the GCF (greatest common factor).
ex: x^2 + 8x -12
= (x-6) (x-2)
for practice I liked using the warmup link she left on her edublog :
https://www.thatquiz.org/tq-0/?-jh00-l7-mpnv600-nk-ppnv600
In week 9 of math 10 we revisited the past by looking at what we learned about polynomials in grade 9. Most of the week was based on reviewing and reminding our brains of what we did, which I had to re-teach myself a bit of the missing parts. We learned about the different types of binomials, trinomials, monomials, etc. we learned how to add like terms and resolve the question to our best abilities. We used grids and diagrams to assist us in resolving questions and we also used foil (finding the product of the first, outside, inside then last terms.) Ms. Burton taught us foil kind of like a claw method so everything multiplies with everything in the opposite bracket.
(4a+7) (2a+2)
- 4a x 2a= 8a^2
- 4a x 2= 8a
- 7 x 2a= 14a
- 7 x 2=14
- combine like terms
- 8a^2 +22a + 14

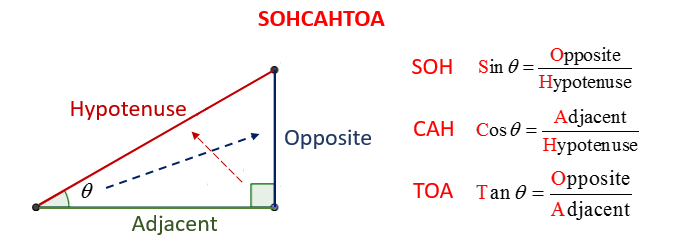
In week 8 of math 10 I found that most of the question I understood except for myself the word problems were confusing at first and I needed assistance with some of them but other than that most of them were just using common sense to find the answered and remembering what SOH CAH TOA stood for (sin using opposite and hypotenuse, cos using adjacent and hypotenuse, and tan using opposite and adjacent.) and how to use it, we needed to learn how to find the missing length and or missing degree for a right triangle. For myself once I wrote down the angles and degrees I knew on a drawing of a right triangle I could tell exactly what to do. A^2 + B^2 = C^2 also known as Pythegoreon theory also helped in finding these answers.