This week I learned how to factor a simple polynomial. A simple polynomial means the leading coefficient is a one. To factor a simple polynomial you need to know what factoring is. Factoring is finding all the different numbers that multiply to get a certain number. Ex. 24 the factors of 24 are 1,2,3,4,6,8,12,24. Now I can teach you how to factor a simple polynomial.

Ex.  + 8x +12

Step one: Factor the constant.

Step Two : Look at the clues; which of the pairs subtract or add to give you the middle term. 

In this case it would be 2 and 6. Another clue is that everything is positive so the factors will be positive.

Step Three: Start writing it out

*You know that x times x is  so the x’s will go at the front of the brackets. (x___)(x___)

The answer is (x +2) (x +6)

To check your answer use the claw method.

THERE IS A VIDEO BELOW TO SHOW YOU HOW TO USE THE CLAW METHOD, ALSO KNOWN AS FOIL

 

 

This week I learned how to find the GCF of a polynomial. This post will teach you how understand how to find the answer.  It seems very complicated at first but if you give it a chance you will learn very quickly. It is not as hard as it seems.

Ex. 9ab – 12ac

Step 1: Start with the numbers and find the greatest common factor. 

*The greatest common factor of 9 and 12 would be 3. 3 x 4 = 12 and 3 x 3 equals 9.

1. Divide by the GCF and bring the 3 to the to the front of the brackets.

Step 2: Move to the variables. Start with the beginning of the alphabet

*Subtract the a with the lowest exponent from the rest of the a’s. Remember that a variable with no exponent has an invisible one.

* remember to bring the a with the lowest exponent out into the front of the brackets. If there is only one of the same variable then you just leave it because it is not common in both. It will be in the left overs.

Step 3: Repeat step 2 with the other variables if possible. 

See Pictures Below 🙂

 

This week we started polynomials. The first time you look at polynomials you will probably have a heart attack. But they’re not as hard as you think. In this post I will teach you what a polynomial is and some vocabulary as well as how to do a question.

Vocabulary:

Type– Types of polynomials

   Monomial- Consisting of one term.

 Binomial- An algebraic expression of the sum or the difference of two terms.

 Trinomial-  An algebraic expression of the sum or the difference of three terms.

 Polynomial- More than three parts/terms in the question.

Degree– The highest exponent

Coefficient-The number in front of a variable.

Constant- In Algebra, a constant is a number on its own.

 

Ex. 3 – 2x + 7y + 4y – 2x + 8z – 9

Step one: highlight or underline like terms to start grouping. 

*like terms are numbers with the same ending.

3 – 2x + 7y + 4y – 2x + 8z – 9

Step two: Rearrange the numbers starting with the letter that comes first in the alphabet then go towards z. Do the constants last. Also go from greatest to least to stay organized.

– 2x – 2x  + 7y + 4y + 8z + 3 – 9

Step three: Combine like terms.

– 4x + 11y + 8z – 6

Type: This equation is a polynomial because it has more than three terms.

Coefficients: -4, 11, 8 *the coefficients poses the sign before it. (+/-)

Degree: If they don’t have an exponent the degree will be one. The only one without the exponent as 1 will be the constant. The constant will have an exponent of 0.

Constant: -6

 

This weeks goal is to teach you how to solve an angle and side lengths in the Trigonometry Unit.

Vocabulary:

SOH: S =  or Sine =  

CAH: C = 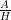 or Cosine =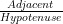 

TOA: = 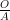 or Tangent =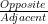 

 

i) Question One: What is the Angle of JEP to the nearest degree? (How to find an angle knowing two side lengths)

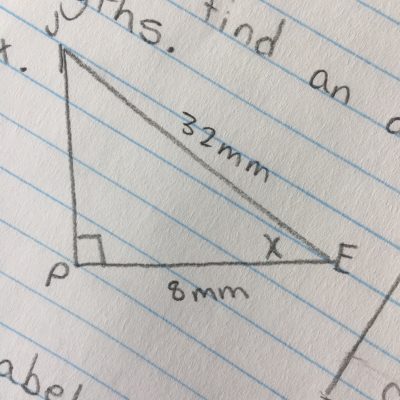Step 1: Label the triangle 

*According to the reference angle

1. Across from the reference angle is called the opposite side (O)
2. Across from the  angle is the hypotenuse (H)
3. And the left over side is the adjacent side (A)

 

 

 

 

 

 

 

Step 2: Determine which ratio to use

Use the clues from the triangle. We will be using Cosine because we have the clues from the Adjacent and hypotenuse sides. (CAH)

 

 

 

 

 

 

 

 

 

 

 

 

Step 3: Write the equation

The cos angle is unknown so we will be writing it like :

 

Step 4: Get the variable by itself/Solve

*when moving the COS to the other side of the equation it becomes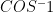 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ii) Question two: What is the side length of AP to the nearest degree. (How to find the side length of a triangle knowing one side length and one angle.)

 

 

 

 

 

 

 

 

 

Step 1: Label the Triangle

*According to the reference angle

 

 

 

 

 

 

 

 

 

 

 

Step 2: Determine the ratio

Use the clues from the triangle. We will be using Tangent because we have the clues from the adjacent and opposite sides. (TOA)

 

Step 3: Write the equation/Solve

*We don’t want the variable on the bottom. Reciprocate the fraction and what you do to one side you do to the other.

 

 

 

 

 

X= 50cm  

 

 

 

 

iii) Question Three: What is the side length of AK to the nearest degree. (How to find the side length knowing one side length and one angle .)

Step 1: Label the Triangle

*According to the reference angle

 

 

 

 

 

 

 

Step 2: Determine the ratio

Use the clues from the triangle. We will be using Sine because we have the clues from the hypotenuse and opposite sides. (SOH)

 

 

 

 

 

 

 

Step 3: Write the equation/Solve

 

 

 

 

*We don’t want the variable on the bottom. Reciprocate the fraction and what you do to one side you do to the other.

 

X= 51 cm

 

This week I partnered with my friend Keisha, and we built a triangular prism 🙂

Here is our work and our end product!

   

This week I learned some pretty cool connections between different shapes. I thought that it was so cool that everyone else should know them. This may even help you in the future with volume.

*All of the shapes have to have to same height and radius/width for this to be accurate*

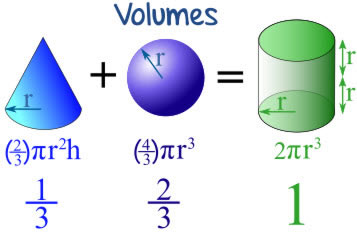One cone with + One Sphere = The volume of a cylinder

 

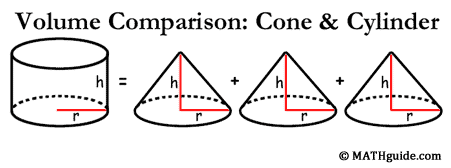 Three cones = the volume of a cylinder

 

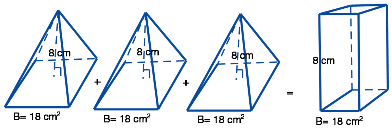 Three pyramids = A Square/rectangle