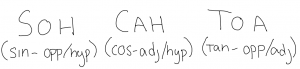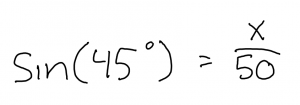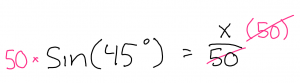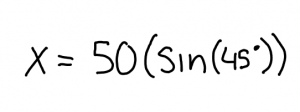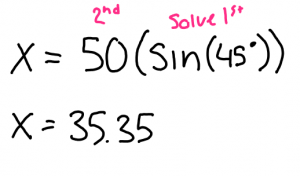This week in class we learned how to find a side in a right triangle. All you need to find a missing side is 1 side and 1 angle.

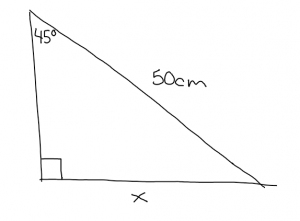
The picture above is an example of a question asking to figure out the missing side.

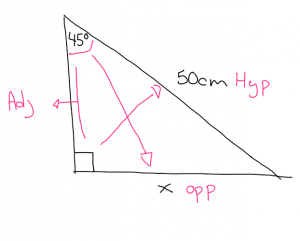
The first thing you should always do is label the sides in respect to the indicated angle.

Once all your sides are labeled you then have to decide what sine ratio you need to use. A trick to remember what sine ratio is appropriate for each question is SOH CAH TOA.

For my example I will be using SIN because the adjacent side does not yet have a measurement.

Once all my sides were labeled I put the numbers into an equation.

The picture above shows how I canceled the denominator (50cm) on the right side and am multiplying 50 onto the left side. Doing this it leaves the right side as x so you can solve for x.

The equation has been written out so you can clearly see how to solve it.

By using the appropriate sine ratio I was able to solve for X.

Last week In class we learned how to convert units of measurements.

We practiced converting between,

SI ( metric ) and SI – Imperial and Imperial – SI to Imperial.

SI is the measurement system that we use in Canada. (cm, m, km…)

The Imperial system is used in the States. (in, ft, yrd, mi…)

conversion ex.

Something I learned this week in math class was Flower power. Flower power is a technique we learned to find how to make a fraction exponent into a radical. After learning this technique, the concept of this math became easier.

Flower power tells you where the numerator and denominator of the exponent goes when you convert it into a radical.

in the pictures above it explains that the denominator refers to the root of the flower making the 6 the root of the radical. the numerator is at the top, it refers to the flower (flower power) that means that the 4 is the power of the number.

In math class we learned how to find the lowest common multiple (LCM) and greatest common factor (GCF) using prime factorization. Essentially prime factorization is all of the prime factors of a number that multiply together to create the whole number.

LCM: Lowest common multiple is a number which 2 numbers can evenly be multiplied to, ex. 4,6. The lowest common multiple of 4 and 6 is 12 (4×3=12) (6×2=12).

GCF: Greatest common factor is a number which evenly divides 2 numbers, ex. 4, 6. The greatest common factor of 4 and 6 is 2 (4/2=2) (6/3=2)

ex. a)   b)

In a) the under lined numbers are all the prime factors, in b) the numbers along the left side of the line are the prime factors. In both a) and b) they show the 2 methods of prime factorization that we learned in class. This step is not showing how to finish finding the GCF or the LCM.

This project wanted us to find a different way aside from prime factorization to solve GCF and LCM.

The method I used to find the greatest common factor and lowest common multiple is by finding and listing all of the divisible factors of the 2 numbers and comparing to see the greatest common factor.

GCF ex.

125: 1 5 25 125

100: 1 2 4 5 10 20 25 50 100

To find the lowest common multiple I took 2 numbers and multiplied them in order starting from 1- 6, although this method doesn’t use prime factorization to do it was still successful.

LCM ex.

125: 250 375 500

100: 200 300 400 500 600 700…

Even with this new method I would still prefer to use prime factorization to figure out LCM and GCF, in my opinion it is easier to find LCM and GCF using prime factorization.