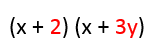November 2016 – Jerrico's Blog

For this project, I was supposed to do some sort of journal depicting a person who migrated to Canada during the Great Migration. I impersonated a Black slave whilst writing letters as to present his journey to achieve freedom from being a slave. The most successful thing I’ve done in this project is, I think, the feelings that was portrayed from the letters. If I were to be given a chance to modify the letters, I would change the first part as it was a bit cheesy. While I was in the process of writing the letters, I learned some things but I think the most important of them is the moral value that I grasped – that I should be satisfied with what I have as others might not have them or have difficulties having them, and if I am not satisfied, then I should work hard as to achieve it. Another thing I’ve learned is that living in the past is harder than we think, there might be some happy people, but there were a lot of conflicts. Nonetheless, I had fun impersonating a person I never thought I would ant it was nice thinking about their perspectives.

One of the things I learned in Math 10 this week is multiplying two binomials. There are a lot of methods to use but the most efficient method is FOIL Method; or First, Outer, Inner, Last.

To do the FOIL method, first, find out if you’re multiplying a polynomial with two terms each. E.g.

So now, we have two binomials that we can multiply. (x + 2)(x + 3y)

How does the FOIL method works? First, you need to know what terms are First, Outer, Inner, and Last.

. So, how do you determine which is which? The first terms are obviously the first terms in each polynomial. In our example it is x and x. The outer terms are the terms ‘outside’ or the ones in both ends of your equation/expression. In our given example, they are the terms x and 3y. The inner terms are the terms ‘inside’ or the two terms in the center of your equation. In our example, they are 2 and x. Lastly, the last terms are the the second terms in each polynomial. It’s 2 and 3y in the example given.