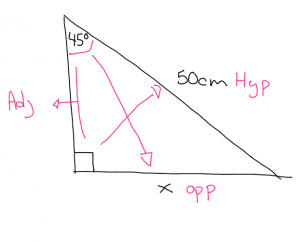
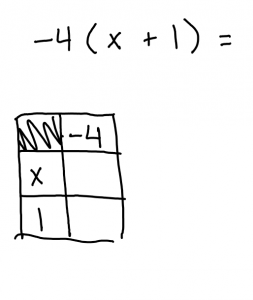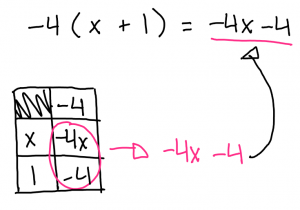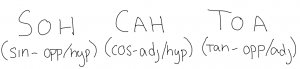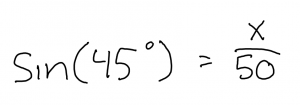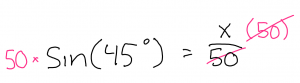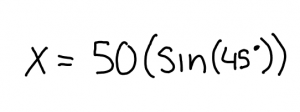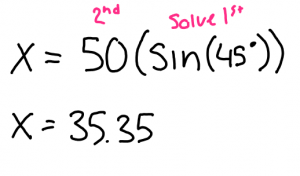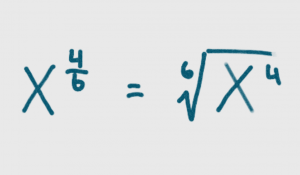Math 10 – Hailey's Blog

Multiplying Polynomials Using Diagrams

By haileys2015

On November 7, 2016

This week in math we learned how to multiply polynomials using diagrams.

There are 2 different kinds of diagrams that we learned. One has algebra tiles and the other one is area diagrams, they are both displayed in a table.

Diagram 1 (algebra tiles)

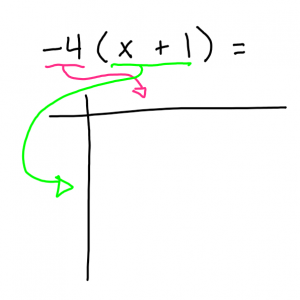
This is an example of a question that you might be given.

You want to start with a table that looks something like this. once you have your table drawn out you need to separate and organize the equation accordingly.

(shaded tiles = positive) (unshaded tiles = negative)

This is the step where you draw out the multiplication. You want to draw the squares and rectangles making sure you line them up properly with the crossing shape.

Keep in mind…
negative x negative = positive
positive x positive = positive
negative x positive = negative

When you write out the final equation you want to make sure you have the proper algebra tiles ( $x^2$ , $x$ , #)

Diagram 2 (area diagram)

This diagram is very similar to the first example but instead of algebra tiles you use the numbers, variables and exponents.

again you start out with an equation that might look something like this.

.

When you put the expressions into the table you want to directly use the numbers and variables.

in this step you want to multiply the crossing variables.

Once you know the values for the inside of the chart you need to take the variables and write them out.

I didn’t have a hard time learning how to do the diagrams, but this was new information to me. If I had to say one thing that might have confused me or made me think hard while using the diagram, the step where you have to determine if the algebra tiles on the inside of the table are positive or negative in the first diagram make me think hard. After a few example/ practice questions I get use to it and it becomes really easy.

If I were to choose which diagram i like using the most I would say diagram 1 (algebra tiles). maybe because I have more practice with them or a greater understanding of how they work but over all they are easier for me to work with.

something about diagram 2 that I really like is that it is a really direct way to figure out the equation, it is quick and easy and really convenient in some situations.

Finding a Missing Side of a Right Triangle

By haileys2015

On October 31, 2016

In Math 10

This week in class we learned how to find a side in a right triangle. All you need to find a missing side is 1 side and 1 angle.

The picture above is an example of a question asking to figure out the missing side.

The first thing you should always do is label the sides in respect to the indicated angle.

Once all your sides are labeled you then have to decide what sine ratio you need to use. A trick to remember what sine ratio is appropriate for each question is SOH CAH TOA.

For my example I will be using SIN because the adjacent side does not yet have a measurement.

Once all my sides were labeled I put the numbers into an equation.

The picture above shows how I canceled the denominator (50cm) on the right side and am multiplying 50 onto the left side. Doing this it leaves the right side as x so you can solve for x.

The equation has been written out so you can clearly see how to solve it.

By using the appropriate sine ratio I was able to solve for X.

Latex Coding

By haileys2015

On October 28, 2016

In Math 10

Ex. 1

$5^2$

Ex. 2

$5^{-1}$

Ex. 3

$\frac{3}{4}$

Ex.4

$\frac{5^2}{3^3}$

Ex. 5

$\tan\theta=\frac{9}{12}$

Ex. 6

$\sin30^\circ=\frac{x}{2}$

Ex. 7

$x=cos^{-1}(\frac{3/4})$

Converting Imperial and SI Units

By haileys2015

On October 12, 2016

In Math 10

Last week In class we learned how to convert units of measurements.

We practiced converting between,

SI ( metric ) and SI – Imperial and Imperial – SI to Imperial.

SI is the measurement system that we use in Canada. (cm, m, km…)

The Imperial system is used in the States. (in, ft, yrd, mi…)

conversion ex.

Flower Power

By haileys2015

On October 4, 2016

In Math 10

Something I learned this week in math class was Flower power. Flower power is a technique we learned to find how to make a fraction exponent into a radical. After learning this technique, the concept of this math became easier.

Flower power tells you where the numerator and denominator of the exponent goes when you convert it into a radical.

in the pictures above it explains that the denominator refers to the root of the flower making the 6 the root of the radical. the numerator is at the top, it refers to the flower (flower power) that means that the 4 is the power of the number.

GCF/LCM

By haileys2015

On September 16, 2016

In Math 10

In math class we learned how to find the lowest common multiple (LCM) and greatest common factor (GCF) using prime factorization. Essentially prime factorization is all of the prime factors of a number that multiply together to create the whole number.

LCM: Lowest common multiple is a number which 2 numbers can evenly be multiplied to, ex. 4,6. The lowest common multiple of 4 and 6 is 12 (4×3=12) (6×2=12).

GCF: Greatest common factor is a number which evenly divides 2 numbers, ex. 4, 6. The greatest common factor of 4 and 6 is 2 (4/2=2) (6/3=2)

ex. a) b)

In a) the under lined numbers are all the prime factors, in b) the numbers along the left side of the line are the prime factors. In both a) and b) they show the 2 methods of prime factorization that we learned in class. This step is not showing how to finish finding the GCF or the LCM.

This project wanted us to find a different way aside from prime factorization to solve GCF and LCM.

The method I used to find the greatest common factor and lowest common multiple is by finding and listing all of the divisible factors of the 2 numbers and comparing to see the greatest common factor.

GCF ex.

125: 1 5 25 125

100: 1 2 4 5 10 20 25 50 100

To find the lowest common multiple I took 2 numbers and multiplied them in order starting from 1- 6, although this method doesn’t use prime factorization to do it was still successful.

LCM ex.

125: 250 375 500

100: 200 300 400 500 600 700…

Even with this new method I would still prefer to use prime factorization to figure out LCM and GCF, in my opinion it is easier to find LCM and GCF using prime factorization.

Hailey's Blog

My Riverside Rapid Digital Portfolio

Category: Math 10

Multiplying Polynomials Using Diagrams

Finding a Missing Side of a Right Triangle

Latex Coding

Converting Imperial and SI Units

Flower Power

GCF/LCM

Recent Posts

Categories

Archives