This week in Precalc 11, we learned a bunch of new things but solving radical equations were the hardest and most confusing for me. I’ve always struggled dealing with negatives, and obviously these radical equations had negatives.
Working step by step is very important while doing radical equations, I learned this week that finding out the restriction for the variable is very important and should be your first step.
Example : pg147, #7c
–
=
The first time I did this question, I did not verify the restrictions and only tried to solve the equation which led me to this answer…
On my second step, I forgot that that negative represented a -1, but instead I just left it there thinking it was a part of the
Now looking back it doesn’t really make sense but my final x value ended up being a negative which was not the right answer
The second time I did the question, I found the restriction of x first and then solved the equation…
Since I found the restriction that x was greater than or equal to 0, I knew the value of x couldn’t be a negative. So I reevaluated the question to see what I did wrong.
In conclusion this week I learned that finding the restrictions in solving radical equations is key, I also re learned that in those situations, the negative is not a part of the root, it represents a -1. Every week I always learn something new and refresh my memory on old concepts.
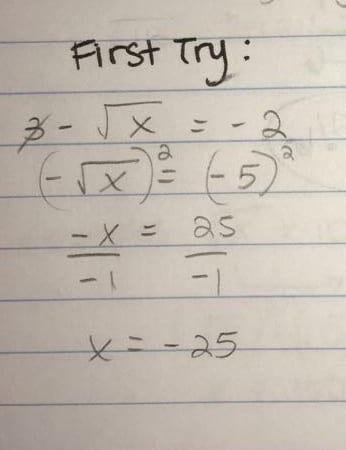


Leave a Reply