This week in precalc we learned how to analyze quadratic functions. We also learned how to use desmos to graph and see how parent functions transform. A quadratic function is written y = a + bx + c .

*Note the difference between equations and functions.*

Equations: you can solve and find roots.

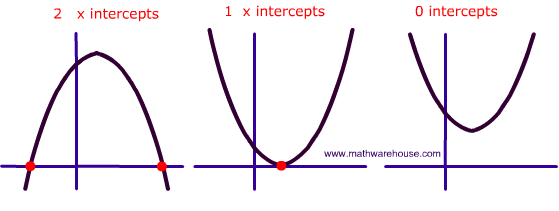
Functions: you can graph, and find Y-intercepts and X-intercepts.

The parabola is the curve where any point is at an equal distance from. The vertex is the highest/lowest point, it may be a minimum or maximum point. The line of symmetry is the line that divides the parabola into mirror images.

When analyzing quadratic functions in a graph, we always need to look for the y-intercept, the x-intercept, the domain and range, parabola, vertex, line of symmetry, if it’s opening down or up, and if it’s congruent to the parent function.

How do we know how parent functions transform:

here’s the video and the link to the website that helped me understand how parent functions transform:

https://youtu.be/dJLQ8UOIuZ4  https://www.purplemath.com/modules/fcntrans.htm

On week 7 we learned a little about the discriminant, and the formula used is – 4ac . It helps determining how many solutions and real roots an equation has. The discriminant is pretty much the number you get under the square root in the quadratic formula.

If the answer to the equation is more than 0 there are 2 solutions, two distinctive real roots.

If the answer to the equation is equal to 0, then there is 1 solution (2 equal solutions), one real root.

If the answer to the equation is less than 0, there are no solutions, no real roots.

1.) 2 solutions

2.) 1 solution or 2 equal solutions

3.) no solutions

This week in precalc 11 we learned how to use the zero product law, which just simply means that if ab = 0, then either a = 0 or b = 0, or both. Let’s say for example we have + x – 30 = 0. First we factor the left side, ( x + 6 ) (x – 5 ) = 0 , now we use the zero product law, being x + 6 = 0 ,  and x – 5 = 0. Now we just simply solve this like any other equation and isolate X, and the final answer is either x = – 6 or x = 5 (these are the two solutions of the equation)

We also learned how to use square roots to solve quadratic equations, also called completing the square. This usually happens when the equation doesn’t factor, but luckily there are 3 steps you can use to do so. First, you take the middle term, then you divide it in half and finally, you square it.

Let’s say for example, we have + 6x + __

First we identify the middle term, which is 6x. Then we divide it in half, giving us 3, and then you just square it, giving us 9.  At the end, the whole equation looks like this:

+ 6x + 9

This week in precalc 11 we did some factoring review.  There were 5 terms we learned:

C- common: a good example that helped me understand this was 15 – 5 = 5 (  3 – 1 )

D- difference of squares (binomials): an example that helped me understand this was ( – 64 ) = ( x + 8 ) ( x – 8 )  *they are like conjugates.

P- patterns (trinomials) : this one is a bit harder but after some practice it becomes easier. First you need to identify each number with the formula  + bx + c, then you need to write down all factors pairs for c, and then you need to find a factor pair that sums up to b, and finally you substitute factor pairs into two binomials

E- easy patterns: an example that helped me understand this one is  + 12x + 35 = ( x + 5 ) ( x + 7 )

U- ugly patterns: all the ugly polynomials that seem hard or just ugly in general: 5 – 7x + 2. For these, we learned to solve them using the box method.