This week in precalc 11, we learned how to add and subtract radicals. The steps do to so are pretty easy. First, we simplify the radicals in the problem, and then we need to make sure the indices and the radicands is the same. If they are the same, you add or subtract the coefficients with the coefficients, and the radicands just stay the same.

Just remember though, if the radicands are not the same, you can’t add or subtract them together.

An example that helped me understand this was:

+ –

Simplify the terms:

7  + 5 – 3 

Add the coefficients together, and leave the same coefficient:

= 7 + 5 – 3 = 9

All you have to remember is to always simplify the radicals, it will make your life way easier!

This week in precalc 11 we learned about the absolute value of a real number.

The absolute value is  the principal square root of a number, it is the distance from a to 0 on the number line. The absolute value is always positive. The sign used to represent it is | |.

For example, let’s say we’re trying to find the absolute value of | -39 | = 39 because the distance between -39 is 39 (the number has to be positive). Another example would be | 24 | = 24  which means that the distance between 24 and 0 is 24.

The absolute value bars do not work like parenthesis or brackets. For example, if you want to simplify – | -25 |.

Because the absolute value of negative 25 is positive 25, we end up with negative positive 25, which at the end gives us negative 25.

– | – 25 | = – ( +25 ) = -25

This week in precalc 11 we learned about geometric series.

Geometric series is the sum of the terms of a geometric sequences, a series with a constant ratio between successive terms. For example, a geometric series would be 6 + 12 + 24 + 48 + . . . The common ratio is the ratio between two numbers in a geometric sequence. To determine the common ratio, you can just divide each number from the number preceding it in the sequence (formula: r = a(n) / a(n – 1) ).

We also learned how the formula for determining the sum of the first n terms in any geometric series using the formula: 

Here’s an example on how to apply this

↓

Find for the geometric series 80 + 60 + 45. . .

a = 80

r = 0.75

= 80 ( ( ) – 1) ÷ ( o.75 – 1)

= 301.98

Another example       ↓

For the geometric series 3, 9, 27. . . 6561, determine how many terms it has and then calculate its sum.

r = 3

a = 3

= 6561

= a (

6561 = 3 ( 

2187 = (

= 

7 = n – 1

8 = n

= 3 (   – 1 ) ÷  ( 3 – 1)

= 9840

One of the things I learned this week in precalc 11 was arithmetic sequences.

An arithmetic sequence is when you have a list of numbers following a certain pattern, where each number increases (or decreases) by adding the same value each time. For example, 3,6,9,12,15… it’s a sequence because each time it adds up to 3. The common difference is the difference between 2 numbers in the arithmetic sequence.

The equation to find the common difference, also known as D, is d = t(n) – t(n – 1) where T means term, N means the last number in the sequence and N-1 means the number before the last one in the sequence. The common difference could be negative, which means that the sequence is decreasing, or it could be positive which means that the sequence is increasing.

We also learned how to define the pattern in a sequence by using the formula:    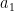              =   + (n – 1) ⋅ d

Here’s an example on how to apply this

↓

Let’s say we want to find the 15th term in the sequence 3,6,9,12,15…

First, we start by identifying our clues to solve this problem. We know that the first term is 3, and we know that the common difference is 3 (because each time the number increases by 3, to prove it we simply just subtract the second term to the first, and to verify we could also subtract the fourth term to the third). So now we just fill in the numbers in the formula and solve.

Here’s another example. Let’s say we want to find out how many terms are in this sequence: 4,0,-4,-8,-12,……..-36. Like before, we start by identifying the clues we have.

We know that our first term is 4, and we know that our last term is -36. We also know that our sequence is decreasing by -4 each time.  Now we fill in the numbers in the formula and solve.

I really enjoyed the first lesson in math because it was amazing learning how we can figure out the terms in any sequence by just using a formula instead of counting and adding until we get there.