 This week was the first week of Pre Calculus 11 for me. So far it has been good, as we are learning about series and sequences. Today I am going to teach you the difference between arithmetic sequences and an arithmetic series. I will also show the formula to find the nth-term and how to find the sum of the terms. STAY TUNED 🙂
This week was the first week of Pre Calculus 11 for me. So far it has been good, as we are learning about series and sequences. Today I am going to teach you the difference between arithmetic sequences and an arithmetic series. I will also show the formula to find the nth-term and how to find the sum of the terms. STAY TUNED 🙂
A SEQUENCE for example, is a set of numbers that are changing in some way.
ex/ 5, 10, 20, 40, 80
5 is called 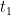 , 10 =
, 10 = 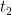 , 15 =
, 15 = 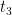 and so on. The t stands for term.
and so on. The t stands for term.
An ARITHMETIC SEQUENCE is a sequence that changes by a constant amount. The constant amount is also known as the common difference.
ex/ 5, 10, 15, 20, 25, d=+5 ;The common difference is +5
to find the common difference the formula is 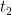 –
– 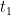
 NOT ARITHMETIC, NO CONSTANT DIFFERENCE
NOT ARITHMETIC, NO CONSTANT DIFFERENCE
An ARITHMETIC SERIES is the terms of an arithmetic sequence added together. The point is to find the sum of the desired terms.
ex/ 5+10+15+20+25 = 75
How to find the nth-term
Say you wanted to find what 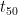 is in the sequence 12, 9, 6, 3, 0 is but you don’t want to continue writing the whole sequence out. Well your in luck, there is a fast way.
is in the sequence 12, 9, 6, 3, 0 is but you don’t want to continue writing the whole sequence out. Well your in luck, there is a fast way.
The formula to find the nth-term is 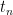 =
= 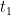 + d(n-1)
+ d(n-1)
- The nth-term is
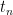 =
= 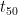
- d= -3
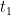 = 12
= 12
Now we insert all the known numbers into the formula
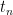 =
= 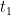 + d(n-1)
+ d(n-1)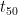 = 12 + (-3)(50-1)
= 12 + (-3)(50-1)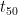 = 12 + (-3)(49)
= 12 + (-3)(49)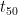 = 12 -147
= 12 -147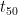 = -135
= -135
There you are, you just figure out how to find the 50th term quick and easy.
How to find the sum of a series
We will take the example from above and determine the sum of  .
.  means
means 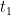 to
to 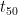 will be added.
will be added.
The formula to determine the sum is 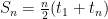
Insert into formula
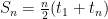
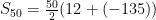
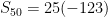
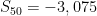
There you have it. Today you learned what an arithmetic sequence and series were, what the formula to find the nth-term and the sum of a series was, and how to solve. I hope this blog post helps you in your future with practice and studying.









 NOT ARITHMETIC, NO CONSTANT DIFFERENCE
NOT ARITHMETIC, NO CONSTANT DIFFERENCE