Loading...

My Riverside Rapid Digital Portfolio

Browsing category archives: Grade 10

1.2 L’immigration chinoise et la perspective historique

Voici notre débat, Ashiana est personne A et Isabelle est personne B. On a fait 3 profils. Ashiana a fait Amor de Cosmos, qui a gagné son pouvoir politique grâce à son programme anti-asiatique, Isabelle a fait Un immigrant récent de la Chine, qui est arrivé en C-B au moment où tout commence à changer épuis on a fini avec Ashiana qui parle a propos de  Un Sino-Canadien qui avait le droit de vote, mais à qui on a enlevé ce droit après que la C-B s’est joint au Dominion du Canada.

Calculating our Emotions – Math Inquiry 2017

Calculating Emotions-20pgd25

Topic: The topic that I chose for my Inquiry was “calculating emotions” this to me is something that everyone can relate to, as the goal with our inquiry was to find math in a topic that isn’t considered mathematical. I thought that our emotions are something that is relevant to every single person no matter their math background.

Main Questions: In my inquiry I talked about the makeup of emotions, how our brains respond to emotions, dopamine, examples of  emotional equations {we did an interactive piece where everyone had the opportunity to calculate the ration of their anxieties and fears, and finally I talked about how subjective emotions are and the chaos theory of how sensitive these equations are.

Further Questions and Extension: While doing my Inquiry project I became very interested in a lot of branches of emotions and how math can be related in a bunch of different aspects, I came up with the further questions; is it possible to measure the intensity of an emotion?, how many emotions is it possible to feel at once?, how can we chemically relieve addiction and fit our medications specifically to a person and their ratio of emotions? and finally, with all the information we have about a persons life is it possible to calculate how someone is going to feel after a certain experience. My dad actually got me a book on emotions after my project and I have been looking through it and have developed some even further questions based on what I have read; How has the media affected the intensity of our emotions? Are the generations becoming more or less sensitive, how and why?

 

Math Art – Graphing Santa

 

In math class, we were asked to graph Santa on desmos. This is the Santa that I created using different linear relations and functions, by restricting the domain and range I was able to place the shapes in a layout to create a Santa!

 

 

 

 

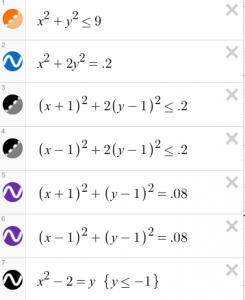 These are the expressions used to create the face:

•The first one x squared plus y squared is a linear relation, not a function used to create the circle. In order to add color, I changed the equal sign to make it an inequality. I chose 9 as the inequality for the size of the face.

•The nose, I left at the origin and just created an oval making the coefficient y not equal to the x coefficient and left it not filled in.

 

•For both the eys I made a small circle and a larger oval to make them a little more realistic. I changed the quadrant of the circle by adding x-1 to the right side and x+1 to the left quadrant to make the eyes on different sides. I made sure they were the exact same numbers to make sure they were symmetrical and proportionally equal.

•For the smile, I used a quadratic function to create a parabola and chose the origin of -2 by adding it as the constant of the equation. For the range, I stopped it at -1 to restrict the smile so that it’s not too high up on the face.

Now, for the add – on’s to the face.

•For the hat, I used an upside-down parabola where x squared equals negative y instead of positive. The constant negative 8 was chosen for the height of the hat. I made the range 2 so that it came up just to the forehead of the shape of the face.

•Then for the line to close up the shape of the hat I just went y=2 so that a horizontal line appeared on the y2 axis. Making sure to add restrictions at -2.5 and 2.5 on either side of the face.

•For the pom-pom at the top of the hat, I created a ball right down the middle of the x-axis and on 9 of the y-axis so it rests just above the hat.

•Finally, for the beard, I made a parabola with the origin of -8 so that it went lower. I made sure to restrict it to a range of -1 so it stops at a good point on the sides of the face.

After doing this activity I feel much more confident with functions and relations and now know mentally what a function would look like if I were to graph it.

Skip to toolbar