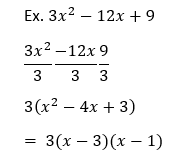This week we finished off our polynomials/factoring unit. Although I did miss a day, I was still able to learn a thing or two that helped me. I learned how to factor polynomials that didn’t have a coefficient of 1. I found the coefficient of 1 polynomials easier than those of a higher leading number, but I still managed to figure it out.

To factor polynomials with a leading coefficient over 1 can be quite easy if done properly. The first thing to do is to check for “CAN DIVERS PEE EASILY UNDERWATER?” which stands for common, difference of squares, pattern, easy, and ugly. So, by following this we should immediately notice that all the numbers have a number in common, 3. We divide each one by 3 to give as an answer of . Now we can answer this like a normal factoring expression. We know that to get , you must put an x in each bracket. To get -4 you must use 3’s only factors, 1 and 3. Both the 1 and 3 must be negative as the positive symbol in front of the +3 indicates that both symbols must be the same. So, our answer would be 3(x-3)(x-1).