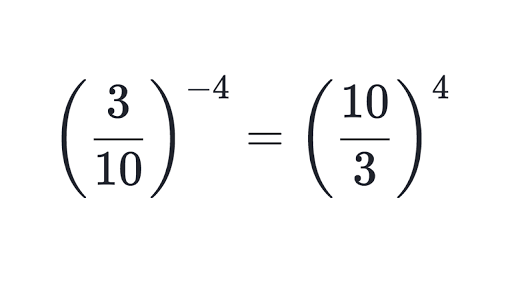November 8, 2019 – Kenya’s Blog

1. Represent repeated multiplication with exponents

When an expression is written in repeated multipcation, it is much easier to take the amount of factors of the base is turned into the exponent. This doesn’t work with 0 though which has a different outcome which is explained in a different question.

Examples: 6x6x6x6= $6^4$ and 3x3x3= $3^3$ .

3. Demonstrate the difference between the exponent and the base by building models of a given power, such as $2^3$ and $3^2$ .

The difference between the base and the exponent is that the base is the original number, while the exponent which is either written in a superscript next to the base and is how many factors of the base in which will be multiplied together.

$6^7$ , the base is 6, the exponent is 7. It can also be written as 6 to the exponent of 7. That would mean 6 x 6 x 6 x 6 x 6 x 6 x 6. The whole thing of $6^7$ /6 to the exponent of 7 is known as the power. Though, $7^6$ is different 7 x 7 x 7 x 7 x 7 x 7.

5. Evaluate powers with integral bases (excluding base 0) and whole number exponents.

When dealing with bases, you will notice bases that are positive and negative. First of all, positive bases go as showed before where you simply multiply the base as many times as the value of the exponent (ex. $6^2$ = 6×6 because the exponent is 2 and you are multiplying two 6’s together. Though, when dealing with negative bases, the answer and whether it is positive or negative depends on if the exponent is even or odd. If you have a negative base and the exponent is even, the negatives will cancel each other out, but if the exponents are odd, then the answer will be negative. (ex. $(-5)^4$ will be 625 while $(-4)^3$ will be -64). There are some interesting situations where you will see a negative power with no brackets around the base( $-6^3$ ) and the outcome to that will always be negative because the negative sign in this expression would be a coefficient because the exponent is inside the brackets. So if you were to write $-6^3$ as a repeated multipication, it would be written as -1 x 6 x 6 x 6.

7. Explain the exponent laws for multiplying and dividing powers with the same base.

When multiplying powers with the same base, you keep the base the same, add the exponents, and if there are coefficients, multiply them.

$2^2$ x $2^4$ = $2^6$ and 3 $(3)^4$ x 2 $(3)^2$ = 6 $(3)^6$

When dividing powers with the same base, you keep the base the same, subtract the exponents, and if there are coefficients, divide them.

$4^7$ $\div$ / $4^5$ = $4^2$ and 6 $(3)^3$ $\div$ 3 $(3)^4$ = 2 $(3)^-1$ = $\frac{2}{3}$ .

9. Explain the law for powers with an exponent of zero.

Anything to the exponent of zero is equal to 1. This is because following the pattern that bases are just multiplied by themselves, they can also be divided by their base to find the number therefore if $2^2$ =4 and 4 $\div$ 2 = 2 and $2^1$ is 2, then $2^0$ must be 1 because $2^1$ = 2 and $\frac{2}{2}$ = 1.

$3^0$ = 1 and $35783297628762967589237^0$ = 1.

11. Explain the law for powers with negative exponents.

When dealing with negative exponents, you have to find the answer as if the exponent was positive and reciprocal it. Don’t just put a one over it because if you are dealing with fractions then you

Image result for exponents

will end up with a complex fraction and an incorrect answer.

$3^-2$ = $\frac{1}{9}$ and $x^-y$ = $\frac{1}{x^y}$ and 2/ $3^-6$ = 2 x $3^6$ .

13. I can apply the exponent laws to powers with both integral and variable bases.

Product Law: When multiplying powers of the same base, you keep the base and add the exponents. If there are coefficients, multiply them. For example, 5 ( $3^2$ ) x 4 ( $3^3$ ) = 20 ( $3^5$ ) = 20 x 243 = 4860 and x $y^a$ *b $y^c$ =xb $y^a$ +c.

Power Law: If there is an equation with one base and two exponents, then the expression is solved differently than regular multiplication. Instead of adding the exponents, you multiply them. For example, ( $5^4$ ) $^3$ = $5^12$ , and ( $x^y$ ) $^z$ = $x^y$ z.

Quotient Law: When dividing powers of the same base, you keep the base and subtract the exponents. If there are coefficients, divide them. For example, 6 $2^3$ $\div$ 2 $2^4$ = 3 $2^-1$ = 3 $\frac{1}{2}$ . and y $x^c$ * b $x^a$ =yb $x^a+c$ .

Negative Exponent Law: You need to reciprocal the answer of the power if the exponent positive. For example, $3^-4$ = $\frac{1}{3^4}$ and $x^-y$ = $\frac{1}{x^y}$ . Also, $\frac{2}{3}^-4$ = $\frac{ 3^4}{2}$ and $\frac{n}{m}^-r$ = $\frac{m^r}{n}$ .

Power of 0 Law: Anything to the exponent of 0 = 1. $3647344327560274363454687067^0=1$ and $x^0$ =1. Also, x cannot equal 0, and $0^0$ does not equal 1.

15. Use the order of operations on expressions with powers.

Remember that you must do brackets first, then exponents. But, if there are exponents inside the bracket, then do the exponents there.

(2 x $3^2$ + 8) / 13

(2 x 9 + 8) / 13

(18 + 8) / 13

26 / 13

= 2

17. Identify the error in applying the order of operations in an incorrect solution.

If you mistake yourself and multiply/divide before applying the power, you will end up with the wrong answer.

(incorrect)

2 $(4)^5$

$8^5$

32768

(correct)

2 $(4)^5$

2(1024)

2048

As you can see, there is a major difference between the two answers.

19. Use powers to solve problems (growth problems)

When doing growth problems, powers are used when showing how much something grew. The amount that you started with would be the coefficient and the base would be how much it grows by per said growing period and the exponent is what changes when the amount of time changes.

A colony of bacteria doubles every hour. There are 50 to begin with. How much will be there after 1 hour? 3 hours? 8 hours? Keep in mind it does not have to be hours. It could be seconds, minutes or even days, months, years, decades, centuries, etc.

So far, you have a consistent amount and how much it goes up by per hour, which is the coefficient and base. It is written like this: 50 x $2^n$ . n=how many hours it has been. So, to find how much there will be in one hour, you would write 50 x $2^1$ . $2^1$ = 2 and 50 x 2 = 100. To find how much there will be in 3 hours, you would write 50 x 2^3. 2^3=8 and 50 x 8= 400. Lastly, to find how much there will be in 8 hours, you would write 50 x $2^8$ . $2^8$ =256 and 50 x 256 = 12800.