In chapter 2, I have learned that Radicals can be simplified through adding and subtracting. The first thing to note is that radicals can only be added and subtracted if they have the same root number. If the radicals in a question are unlike, you won’t be able to combine them together. That’s one of the main rules for radicals that you should remember
How to subtract radicals
Our example will help you grasp the basics of what we mean when we say you have to find like radicals before combining them. The simplifying radicals problem below deals with how to subtract radicals.
Question 1:
√90−√
Solution:
We are going to first simplify this expression. We will perform a division analysis for the number 90 in order to identify its roots:

We learn that √90 can be re-written as:
√5⋅2⋅
Since we are dealing with square roots (which is what a radical sign stands for. There should be a tiny 2 next to the radical sign to indicate that we’re working with square roots, but it is generally accepted to simply write the sign without it), we are looking for numbers in pair. In this case, we can see that we have a pair of 3s

Now, we can take the pair outside of the radical (square root), leaving us with:
3√5⋅2=
This means our question can be transformed into the following expression:
3√10
You can see that we’ve now identified the “like” radicals in the question: 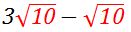 .
.
We can finally do the subtraction, and the result gives us:
2√
To add radicals, the method is the same as subraction the radicand (the number that is under the radical) must be the same for each radical, so, a generic equation will have the form:
ab+cb=(a+c)b
Let’s plug some numbers in place of the variables:
