Category Archives: Math 11
Rational Expressions and Equations
For chapter 6, I learned solving rational expressions and equations which include addition, subtraction, multiplication, and division.
First, rational expressions are defined as a fraction in which the numerator and denominator are polynomials but one thing to note is that the denominator can’t be zero. It cannot contain roots and exponents of variables.
If there is a variable that makes the denominator zero, then it is considered as a non-permissible value.
e.g
x-3/x-5
x cannot be +5 as it will make changes to the denominator to (5-5=0). That’s why +5 is a non-permissible value.
here are the examples of dealing with addition, subtraction, multiplication, and division.
for addition, subtraction, the key point is to find the same denominator as normal fractions, as long as we’ve got the same denominator, then just focus on the upper part.
for multiplication and division, we can just simply apply the strategies for doing normal rational numbers.
One important thing is at the end, all the non-permissible value must be listed out
quadratic functions
Before Christmas, we have to go through chapter 4.
First, there are 3 types quadratic function
- 1) Standard form: y = ax^2 + bx + c where the a,b, and c are numbers.
- 2) Factored form: y = (ax + c)(bx + d) again the a,b,c, and d are numbers.
- 3) Vertex form: y = a(x + b)^2 + c again the a, b, and c are numbers.
My favorite part and I found it interesting is graphing quadratic function
features in a graph :
Vertex
the lowest and highest point of the parabola is called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph or the maximum value.
Axis of Symmetry
Parabolas also have an axis of symmetry, which is parallel to the y-axis. It’s is a vertical line drawn through the vertex.
y-intercept
The y-intercept is the point at which the parabola crosses the y-axis. There cannot be more than one such point, for the graph of a quadratic function. If there were, the curve would not be a function, as there would be two values.
x-intercepts
The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots, of the quadratic function, the values of at which . There may be zero, one, or two -intercepts. The number of x-intercepts varies depending upon the location of the graph.
here is an example of graphing, given a vertex form y= (x-1)^2+1
there is a hidden 1 before (x-1)^2, so it’s positive, the graph opens upwards, x-(+1) makes the graph shift right to (1), x=1. the +1 y= (x-1)^2+1 makes the graph goes upwards (y=1). This is how we graph.
solve quadratic equations
last week, we have learned two ways to solve quadratic equations
the first method is completing the squares
example 1: Solve the equation below using the method of completing the square.

Move the constant to the right side of the equation, while keeping the x-terms on the left. I can do that by subtracting both sides by 14.
Next, identify the coefficient of the linear term (just the x-term) which is

Take that number, divide by 2 and square it.
Add 814 to both sides of the equation, and then simplify.
Express the trinomial on the left side as a square of binomial.
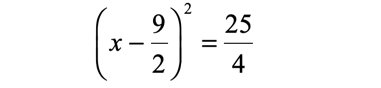
Take the square roots of both sides of the equation to eliminate the power of 2 of the parenthesis. Make sure that you attach the plus or minus symbol to the constant term (right side of equation).
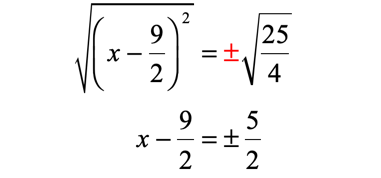
Solve for “x” by adding both sides by 9/2 .
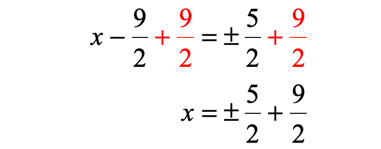
Find the two values of “x” by considering the two cases: positive and negative.
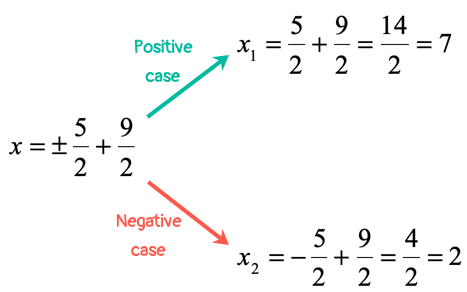
Therefore, the final answers are x= and x. You may back-substitute these two values of from the original equation to check.
for the quadratic formula
substitute for a,b and c in
adding and subtracting radicals
In chapter 2, I have learned that Radicals can be simplified through adding and subtracting. The first thing to note is that radicals can only be added and subtracted if they have the same root number. If the radicals in a question are unlike, you won’t be able to combine them together. That’s one of the main rules for radicals that you should remember
How to subtract radicals
Our example will help you grasp the basics of what we mean when we say you have to find like radicals before combining them. The simplifying radicals problem below deals with how to subtract radicals.
Question 1:
√90−√
Solution:
We are going to first simplify this expression. We will perform a division analysis for the number 90 in order to identify its roots:

We learn that √90 can be re-written as:
√5⋅2⋅
Since we are dealing with square roots (which is what a radical sign stands for. There should be a tiny 2 next to the radical sign to indicate that we’re working with square roots, but it is generally accepted to simply write the sign without it), we are looking for numbers in pair. In this case, we can see that we have a pair of 3s

Now, we can take the pair outside of the radical (square root), leaving us with:
3√5⋅2=
This means our question can be transformed into the following expression:
3√10
You can see that we’ve now identified the “like” radicals in the question: 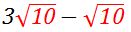 .
.
We can finally do the subtraction, and the result gives us:
2√
To add radicals, the method is the same as subraction the radicand (the number that is under the radical) must be the same for each radical, so, a generic equation will have the form:
ab+cb=(a+c)b
Let’s plug some numbers in place of the variables:
math pre-cal 11
last week, I have get to know more about square roots. One of the skills that we learned is turning mixed radical to entire radical. In order to do this, we need to take the integer number in front of the root sign, which is called the index, and put it under a root sign. In other words, we replace the integer with a radical. Thus, we will end up with two radicals that need to be multiplied. We multiply the two numbers under the roots and place the product under a root sign.
Writing mixed radicals as entire radicals is useful in that in allows us to more easily to determine which radical in a set is largest. As long as the radicals have the same index, then they can be compared by comparing the radicands.
Also, I have learned to deal with a negative exponent. It means to divide by that number of factors instead of multiplying. So 4−3 is the same as 1/(43), and x−3 = 1/x3







