Day: October 31, 2016

ScienceAppReview- ADL10

Jayden Bawden on

Everyone should be able to have the Periodic Table of Elements at the tip of their fingers for work, schooling and just in case you are being curious. This app would be good if you can personally choose an element to explore and learn it more. I wanted to find an app that can help you learn and always be able to visually see the Periodic Table and always have it with you.

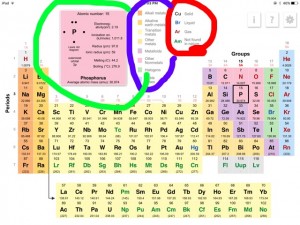
The app I found and used is called K12 Periodic Table. I would highly recommend this app as it allows you to click on any element that you chose and allows you to see its Electronegativity (1) Ionization (2) Radius (3) Melting Point (4) Boiling Point (5) Symbol (6) Name (7) Average Atomic Mass (8) Atomic Number (9). This app states and shows the Alkali Metals, Alkali Earth Metals, Transition Metals, Other Metals, Metalloids, Other Nonmetals, Halogens and Noble Gases. Along with columns of explain what each colour of symbol meant, Ex. Black= Solids, Blue= Liquids, Red= Gases and Green= Not Found in Nature.

Jayden Bawden.

img_1532 img_1531

Exponent Laws: Blog Post1

Jayden Bawden on

Multiplying powers with the same base you ADD the exponents:

-2^2\cdot-2^5 you would then add the exponents as 2+5= 7 the answer is -2^7 .

Dividing powers with the same base you SUBTRACT the exponents:

\frac{5^3}{5^5} so, 5-3=2 therefore the answer would be 5^2

When you have an equation and it has brackets with a base and a exponent but also and exponent outside the brackets you MULTIPLY both of the exponents together, then add the answer you got to the base as the new exponent:

(5^4)^2 you multiply 4 by 2 to get 8, therefore  5^8 is your final answer.

When you have a multiplication question in brackets with an exponent outside of the braces you can REWRITE the two bases with the exponent:

2×3^3 you would give both bases a 3, 3^3 2^3 would equal 27 x 8= 216.

To find the power of a question that is a division question in brackets with an exponent outside you TAKE AWAY the brackets and ADD the exponent to each base:

\frac{5}{6}^3 would turn into \frac{5^3}{6^3} because we add the exponent to both bases.

When you have a addition question with exponents you SUBTRACT, however when you subtract the same exponent it becomes ZERO. So, when you have an exponent of zero it will ALWAYS be 1.

5^4+5^4 you subtract 4 by 4 to get 0 therefore its 5^0 .

Jayden Bawden