
1. Represent repeated multiplication with exponent
If you had a question that asked you what is equal to  that’s just a more difficult way of saying
that’s just a more difficult way of saying 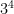 . its a form of
. its a form of  .
.

=
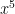
2.Describe how powers explain multiplication
Exponents are a faster form of repeated multiplication, just as multiplication is a faster form of repeated addition, some examples are
x+x+x+x =

, and exponents are

=
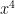
so anything to an exponent is just the

multiplied the by itself the amount of time as represented by the exponent
3. Demonstrate the difference between the exponents and the base by building models of a power.
this is an example of
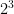
or 2 cubed
each side is 2 units long, so
its like saying

and that’s the same as saying
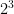

This is the flipped version of
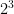
,
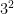
. as you can see it has gone from a cube to a 2 dimensional shape which is another reason why the base and the exponent CAN NOT BE SWITCHED.
4. Demonstrate the difference two given powers in which the exponent and the base are interchanged by using repeated multiplication
The

and the

are two completely different things. The base is the bottem part of the

and the number that is being multiplied, the exponent is the top number in the power that is how many times you multiply the base.
THEY ARE NOT INTERCHANGEABLE

=

= 8

=

= 9
5. Explain the role of parentheses in powers

are very important when it comes to powers with negative bases. The difference between
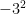
,

and

important.
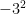
in repeated multiplication is

which is equal to -9, meanwhile

in repeated multiplication is

which is equal to 9. The third

is the same as
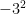
, just inside parentheses. if you get these things confused then you will end up with 2 completely different numbers. Parentheses also have their regular use of grouping things together as in P.E.D.M.A.S.
6. Evaluating exponents with integral bases and whole number exponents
When we are doing exponents with negative bases remember that if the exponent is even the answer will be positive and if it’s odd then the answer is negative. This rule only works for negative exponents inside parentheses. an example of this is:
 = 81
= 81
 = -27
= -27
 = -81
= -81
 = -27
= -27
7. Explain the exponent law for multiplying and dividing powers with the same base.
When 2 powers have the same base, their exponents can be manipulated before you solve for the power. the 2 laws here are the 
 , and the
, and the 
 .
.
The product law is when both power’s bases are the same, you can add the exponents so  would be equal to
would be equal to  .
.
The quotient law is when both powers have the same bases, their exponents can be subtracted  would be equal to
would be equal to 
8. explain the law of raising a power to an exponent
if you get a question that looks like this  . this means you have to use the
. this means you have to use the 
 . the power law says that if you an exponent outside parentheses containing a power, then you can keep the base and multiply the exponents, so
. the power law says that if you an exponent outside parentheses containing a power, then you can keep the base and multiply the exponents, so  would be equal to
would be equal to  .
.
9. explain the exponent law for raising a quotient and a product to an exponent.
the quotient law and product law are above but here they are again,
The product law is when both power’s bases are the same, you can add the exponents and then multiply the  (if there are any) so
(if there are any) so  would be equal to
would be equal to  .
.
The quotient law is when both powers have the same bases, their exponents can be subtracted, then divide the coefficients (if there are any)  would be equal to
would be equal to 
here is an example:
 first you would add the exponents from 3 to the power of 4 and 3 to the power of 5,then subtract the exponents from 3 to the power of 7. this gives you
first you would add the exponents from 3 to the power of 4 and 3 to the power of 5,then subtract the exponents from 3 to the power of 7. this gives you 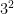 . notice how the base didn’t change throughout the whole thing.
. notice how the base didn’t change throughout the whole thing.
10. explain the law for powers with the exponent of zero
first any base with an exponent of 0 is equal to 1. this works because while 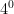 = 1 may not make sense at first there is a way to prove it. if you use PEDMAS the in the expression
= 1 may not make sense at first there is a way to prove it. if you use PEDMAS the in the expression
 =
=  which is 1.
which is 1.
so if  is the same thing, the logically its equal to 1
is the same thing, the logically its equal to 1
11. use patterns to explain the zero law
observe:
 = 32
= 32
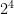 = 16
= 16
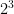 = 8
= 8
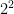 = 4
= 4
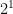 = 2
= 2
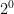 = 1
= 1
the pattern is that each time the numbers divide by 2 so if
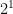
is equal to 1, then logically the next one down
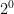
should be 1.
12. Identify the error in the simplification of an expression using exponents
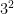
= 6
the student who did this preformed

instead of


= $latex 3^6
instead of adding using the product law like you are supposed to, the student multiplied the exponents.
13.apply the laws of exponents
product law

=

Quotient law

=
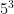
power law

=
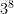
zero law
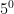
= 1
negative law

=

14. use order of operations on expressions with powers.
order of operations or PEDMAS is used on expressions where exponents are being added or subtracted as there is no way to do it in the form of a power
so in the expression:
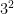
+
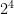
you would do the exponents first turning it to 9+16 = 23
or now one that’s more complicated.
Answer:
you have to work it out in the order of operations.
first do the brackets, and inside use PEDMAS again and solve the exponent then subtract 4, making it 9-4=5, and now our question looks like
15. identify the sum and difference of 2 powers
you have to convert both to fractions first then add or subtract them
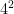
+
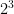
= 16 + 8= 24
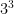
–
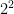
= 27 – 4 = 23
16. identify the error in applying the order of operations with the incorrect solutions
a student answered this equation
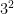
–

= 1
what the student did is he added the exponents on the multiplication right, but then did 3 squared divided by 3 squared when he should have done 9-9 which is 0 not 1
17 and 19. use powers to and order of operations to solve problems(growth)
for the next 2 questions, a) is the powers problem and b) is the order of operations and powers part
write an expression using powers to solve the problem, then solve it.
a) if a single virus cell infected an animal, and it took 1h for that virus cell to corrupt a regular animal cell and multiply itself by 10, how many virus cells would there be in 12h?
Answer:
if a single virus cell infected an animal, and in 1 hour the 1 virus cell turned into 10, then that would be like saying

, so if the exponent is the hours then the expression would just be

and the number of virus cells in 12 hours would be: 1,000,000,000,000 virus cells
b) and if each virus cell can only live for 9h.
that means that any virus cell created past the 3rd hour would live, so the expression would be

–
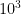
and the amount of cells there are would be 999,999,999,000 virus cells inside the animal
18 and 20. use powers and order of operations to solve problems(measurement)
problem, write an expression using powers to find the area the question asks you for, then solve it.
a) find the total area of the outer square
it is a simple solution as
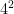
would be the full area of the outer square, because exponents a
can be used to find the area of a square.
the are on the outer square is $latex {16cm}^2
Solution: because they’re both squares you have to subtract the area of the little square from the area of the big square.
so, the expression would be:
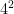
–
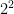
which is
16-4=

21. apply the exponent laws to with coefficients and variable bases
The 5 main laws of exponents are
– the product law
the formula to solving for the product law with coefficients is to have the base of the power stay the same, add the exponents together, and multiply the coefficients
Example:

a and b are coefficients, c and d are exponents and x is the base. the answer is:
– the quotient law
the quotient law is like the opposite of the exponent law, so you would keep the base, subtract the exponents and divide the coefficients
Example:
so the answer would be

$latex x^{y-z}
– the power law
the power law is a simple one
keep the base and multiply the exponents the give the coefficient an exponent of its own, then solve.
Example

=

– the zero law
the zero law is the easiest of them all. any base with a coefficient of 0 is 1
Example:
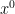
=1
– the negative law
the negative law is probably the hardest of the 5, but there’s a trick to it as well. whenever an exponent is negative in a question, then you have to flip it with a fraction and the power that had the negative exponent now has a positive one, just on the other side of the fraction.
Example

= $latex \frac{1}{x^4}
22. explain the negative exponent law and apply it to both integral and variable bases.
The



is the law that tells you how to deal with negative fractions. if we continue with the pattern from #11 then we see that
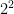
= 4
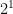
= 2
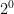
= 1
so if we continue with this pattern…
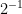
=
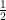
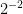
=
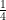

=

and so on and so forth.
another way to think of it is whenever an exponent is negative in a question, then you have to flip it with a fraction and the power that had the negative exponent now has a positive one, just on the other side of the fraction.
Example:

=
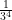
and with variable bases:

=
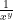
this rule can be easily applied to any power with a negative exponent
23. use the order of operation’s on expressions with powers involving negative exponents, and variable bases.
the answer would be

because the do negatives add together due to the product law, and because of the negative law they must go
to the bottom part of the fraction but 15 doesn’t have a negative exponent, so it stays on top.
-Anything else I know about exponents
any power with a base of 1 equals 1.
that’s just a more difficult way of saying
. its a form of
.
= 81
= -27
= -81
= -27
, and the
.
would be equal to
.
would be equal to
. this means you have to use the
. the power law says that if you an exponent outside parentheses containing a power, then you can keep the base and multiply the exponents, so
would be equal to
.
(if there are any) so
would be equal to
.
would be equal to
 first you would add the exponents from 3 to the power of 4 and 3 to the power of 5,then subtract the exponents from 3 to the power of 7. this gives you
first you would add the exponents from 3 to the power of 4 and 3 to the power of 5,then subtract the exponents from 3 to the power of 7. this gives you . notice how the base didn’t change throughout the whole thing.
= 1 may not make sense at first there is a way to prove it. if you use PEDMAS the in the expression
=
which is 1.
is the same thing, the logically its equal to 1
= 32
= 16
= 8
= 4
= 2
= 1





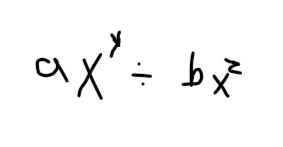

You did a great job on addressing all of the prescribed outcomes for exponents. Your explanations and examples were easy to understand, especially because you added lots of detail in each outcome. It was also made easy to understand you r explanations and examples when you used colours or bold to emphasize the important words. There was an error in 11 (use patterns to explain the zero law). Your explanation was that the numbers descend by 2. But 32 to 16 to 8 to 4 is not descending by 2 it is dividing by 2. Also you didn’t apply the negative exponent law to variable bases in 22, you only explained using integral bases. Other than that I didn’t find any other errors but in 23 I think it would’ve been better to evaluate your order of operations expression by solving and showing each step underneath the expression other than explaining in a paragraph. I thought that your examples in each outcome were well picked out for they really helped with your explanations. I also thought outcome 3 was swell done because you used a long detailed description to help understand the difference between the exponents and the base. Overall I thought your post was very good other than the couple errors.
Hi Adam,
You still need a comment from a parent.