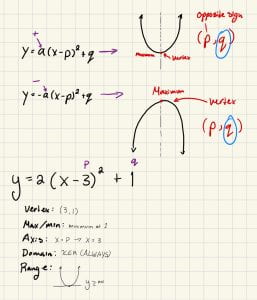
My top five things I have learnt this semester

Studying for Math: I have significantly improved in math compared to previous years, so I think it’s important to share what helped me study. I learned that doing all the questions in the workbook and thoroughly reviewing all the notes from each unit really helped me prepare for tests. Additionally, not having marked quizzes has given me more time to study, which has made math easier.

Vocabulary: My math vocabulary has greatly improved since starting Pre-Calc 11. This is due to the weekly blog posts and the frequent use of terms in class. This has made communicating in math much easier.

Factoring Quadratics: This unit was very helpful in solidifying my factoring skills and helped me understand the subsequent units.

Rational Expressions: Before this unit, I was not good at solving or simplifying fractions. However, after practicing repeatedly and understanding the rules for dividing, multiplying, adding, and subtracting algebraic expressions, I am now more comfortable and confident with these problems.

Trigonometry: This was a confusing unit to learn, but I improved by doing all the questions in the workbook and reviewing notes and skills checks. Although I found this unit challenging, I am glad that I now have a better understanding of it.

This week in pre-calc 11 I learnt  how to use the sCosine law to help find angles and side lengths of triangles. Why this is important? it is because it helps speed up the process of finding an answer compared to what we originally learned in grade 10.

What is the cosine law?

It is also called the cosine rule. If ABC is a triangle, then as per the statement of cosine law, we have: a² = b² + c² – 2bc cos α, where a,b, and c are the sides of triangle and α is the angle between sides b and c.

When to Use the Law of Cosines

1. SSS (Side-Side-Side) Case: When you know the lengths of all three sides of the triangle and need to find one of the angles.
2. SAS (Side-Angle-Side) Case: When you know the lengths of two sides and the measure of the included angle and need to find the length of the third side.

Here are some Examples…

The Law of Cosines is a powerful tool for solving triangles, especially when the Pythagorean Theorem isn’t applicable. By understanding how to apply it, you can solve for unknown sides and angles in a variety of triangle problems.

Hope this helps:)

What I learned this week in trigonometry was how to find reference angles. It is important to know this because it is a basic thing to know and continue to use throughout trigonometry.

How I learned to find the reference angle is through the rotation angle. The rotation angle is the angle formed between the initial arm and the terminal arm. The reference angle is the acute angle formed between the initial arm of the rotation angle and the x-axis.

To find the reference angle it depends on which quadrant (Q) the rotation angle is in. If it is in Q 1, the reference angle is the rotation angle. Q2, you minus the rotation angle from 180°. Q3, minus 180° from the rotation angle. Q4, 360° minus the rotation angle.

To find the reference angle in question a) first you want to determine what quadrant the angle is in from the rotation angle, in this case Q4 and draw an angled line from the middle of the grid to represent the rotation angle. Once you have done that, draw the angle that connects the line you created to the x-axis, this is the reference angle. Next draw an arrow that starts at the terminal arm, and ends at the angled line, this is the rotation. Since the rotation angle is in Q4, you will minus the rotation angle 313° from 360° because 360° is the x-axis angle the rotation angle is attached too. Your final answer will be 47°.

First step to find the reference angle in question b) is to draw the rotation line in the correct quadrant. From there draw the angle that connects the line to the x-axis, this is the angle you are trying to find. Draw the arrow that starts at the terminal angle and ends and the rotation angle, this represents the rotation. Since the rotation angle is in Q3, you will minus the x-axis angle the rotation angle just passed, 180°, from the rotation angle 230°. Your final answer will be 50°.

What I learned this week was one way to solve rational equations is to use cross multiplication. I chose to write about this because sometimes using this method to solve rational equations might be faster and easier than finding a common denominator.

Something to remember when using cross multiplication is that there must be two fractions separated by the equal sign to use this method, but know that you can manipulate a question so that it is set up like this.

To cross multiply, you bring up the denominators and multiply them by the opposite numerators. In this example, you will bring the n minus three up to the other side of the equal sign, and multiply it by two and bring the n up to the other side of the equal sign, and multiply it by six. After you have done this you can solve to find the value of the variable. Remember to add restrictions to the variables in the denominator when needed. The answer is n equals to negative three over two, but cannot equal to zero and three

hope this helps 🙂

This week in Precalc 11 I have learned how to solve for and write non-permissible values for rational expressions.  I chose to display my learning of non-permissible values because when a rational expression is a fraction you never want zero in the denominator, so when stating the non-permissible value you are stating what number cannot be in the denominator that would make it equal to zero. You only write non permissible values if there is a variable in the denominator.

How you can solve is by….

Starting with factoring the denominator, do not simplifier further with the numerator yet, once the denominator is factored state the x values as normally (#’s are going to be opposite when stating it), now write the variable does NOT equal to those numbers, it is very important you remember that you write the ‘does not equal to’ sign because if you forgot you are stating something else entirely.

Down below I have displayed a rational expression and how to solve for the non-permissible values.

This week in Precalc 11, I learnt how to graph inequality problems involving two variables. I decided to write about it because I find it difficult to do and I think that by going over it, I will have a greater understanding of the subject.

The first step to graphing the inequality is knowing the information given to you as the inequality could be written in quadratic or linear form. In this example the inequality is written in linear form and from this we can see that the run and rise is 2, and the y intercept is -3. We can then graph the line. When we have a greater than or less than symbol, we have to shade one side of the line to show that it is the side with possible solutions. To determine which side to shade you can plug in a coordinate into the inequality equation and if it is true, then you shade that side of the line and if it is not, shade the other side. If I plug in (0,0) to the inequality, 0 is not smaller or equal to -3 so this means that I shade the opposite side. The inequality sign also determines if the line of the equation is solid or dashed. It is solid in this example because the sign is equal to, if it is not equal to the line is dashed.

In this example, the inequality is written in quadratic form. First we can determine that the vertex will be placed at (0,-3) and have a stretch value of -5. Graph the parabola. To determine what to shade, it depends on which way the inequality sign faces the Y. For this example, since the inequality sign is indicating y is greater than and the parabola is opening up, you will shade the inside of the parabola because that is where the value of y is highest. You can also use the method above of plugging in a coordinate to determine where to shade. The line is dashed because the inequality sign is not equal to.

hope this helps:)

https://www.desmos.com/

This week in precalc 11, I learnt how to graph and solve one-variable inequalities. I chose this subject because it serves as the foundation for understanding how to draw more complicated inequality graphs, such as those involving two variables.

In this first example, we don’t have to solve the inequality, but we have to graph it. The type of dot you use depends on the greater than or less than sign. If the greater than or less than sign has a line under it, you will use the solid dot as it indicates that x can also be the value, if the sign does not have a line, use a hollow dot as it indicates the value is not included. In this example we will use a solid dot. Place the solid dot on the value of x, 3. To determine where the arrow will point it depends if it is a greater than or less than sign in the inequality. When x is on the left side of the inequality, the sign pointing to the right like an arrow, is greater than, but if it is pointing towards x, left, it is less than. In this case the arrow will point to the left.

For this example, the first thing you want to do is solve the inequality, you do this by isolating the variable x. Something you have to remember when solving inequalities is that when you divide by a negative, you must flip the greater than or less than sign. This is because dividing by a negative makes the greater than or less than sign no longer true to the equation. After isolating the variable, you can then graph the inequality. Figure out the type of dot you will use as explained above and graph it. Next, determine where the arrow will point, in this case it will point to the right.

hope this helps:)

How do you find the transformation of a function?

For a function y = f(x), if a number is being added or subtracted inside the bracket then it is a horizontal translation. If the number is negative then the horizontal transformation is happening to the right side. If the number is positive then the horizontal transformation is happening to the left side.

Definitions

vertex –  is a point where two straight lines meet.

conjugate – A math conjugate is formed by changing the sign between two terms in a binomial. For instance, the conjugate of x + y is x – y.

maximum – a point at which a function’s value is greatest. If the value is greater than or equal to all other function values, it is an absolute maximum.

minimum – The smallest value of a set, function, etc.

domain – is the x values in a function such as f(x)

range – is the y values in a function such as y =.

Function Transformations. Transformation of functions means that the curve representing the graph either “moves to left/right/up/down” or “it expands or compresses” or “it reflects”. For example, the graph of the function f(x) = x² + 3 is obtained by just moving the graph of g(x) = x² by 3 units up.

We can tell this when looking at our equation:

Hope this helps 🙂