Graphing:

This year in precalculus, we have mainly been looking at quadratic function graphs and how the different forms give different information to graph the most accurate parabola.

General form: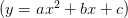

• y-intercept
• slope

Factored form:  () ()

• x-intercepts
• axis of symmetry

Completing the square (standard): +q

• vertex

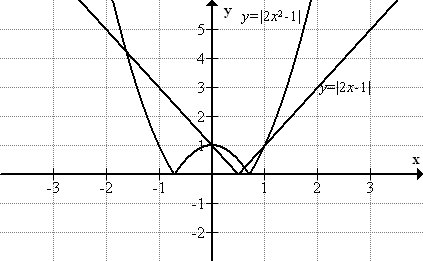
Absolute value function: 

Before I had an idea of what an absolute value function was, but learning and seeing it on a graph gave me a deeper understanding of absolute values.

I learned that a linear absolute value looks like a V and a quadratic function looks like a W. I also learned that the points of inflection are the parts of the graph where the directions change dramatically, and there are two points of infliction in absolute value functions. Lastly, I learned how to write piecewise notation.

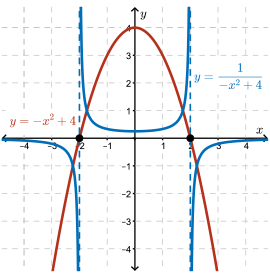
Reciprocal function: 

This unit was one of the most interesting units because I knew that one pair of numbers whose product is 1 when multiplied together is reciprocal, but seeing the visual was something completely new, and I had a lot of fun drawing the graphs for these reciprocal functions, which I had no idea how to do at first.

I learned that invariant points are both 1 and -1 reciprocating into the same number. I also learned that an asymptote is a horizontal, vertical, or slanted line that the lines(hyperbola) approach but never touches, that goes through the x-intercepts.

Rational Expressions: 

Building off of the knowledge from previous years of fractions, we learned about rational expressions.

The main thing that I’ve learned is that it is not possible to simplify the equation by removing a variable by itself and that rational expressions need a Lowest common denominator when adding or subtracting variables. I also learned about non-permissible values, which is the value that makes the denominator of a fraction become a 0, which is undefined.

Trigonometry: 

This year we learned how to find the lengths of sides and the angles of a non right triangle( a triangle that does not consist a 90 degree angle), through the sine, and cosine law.

Sine law can determine an angle or side length with the information of 1 angle and side opposite from each other and another side length or angle. a/sinA = b/sinB = c/sinC

Cosine law can be used when you have 2 sides and an angle or 3 sides. a2 = b2 + c2 – 2bc cos A