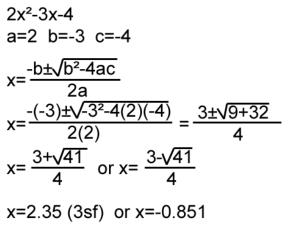Week 6- Solving Quadratic Equations

This week, we learned how to solve quadratic equations by factoring, completing the square, and using the quadratic formula.

Factoring

Factoring and using the zero product property is one of the easiest ways to solve a quadratic formula, and it works with rational roots.

A quadratic equation is any equation that can be written in the form a $x^2$ + bx + c= 0.
Zero product property: if ab=0, then a=0 and b=0, or both a, b=0

example:

3 $x^2$ – 21x- 54= 0

3( $x^2$ – 7x- 18)= 0

(x+2) (x-9)= 0

Either x+2= 0 or x-9= 0

x= -2, x= 9

Completing the Square

When the equation doesn’t factor, completing the square is a great way to solve the quadratic equation, and it works well with irrational roots.

Rearrange the equation if the coefficient of $x^2$ is negative
Make sure to get rid of the coefficient of $x^2$ by dividing each side by the coefficient (when the equation equals to 0)
Move the constant term to the right of the equation
complete the perfect square by dividing the 2nd term and multiplying and squaring it, and adding it to both sides of the equation
factor the perfect square, and simplify the right side
rake the square root of each side, and isolate the x

example:

12x= -2 $x^2$ + 54

2 $x^2$ + 12x= 54

$x^2$ + 6x= 27

$x^2$ + 6x + 9= 27+ 9

√ $(x-3)^2$ = $\pm$ √36

x-3= $\pm$ 6

x= 3 $\pm$ 6

Quadratic Formula

The Quadratic formula is easy to use if it is arranged in the right form.

example:

Joy's Blog