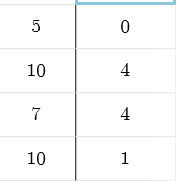
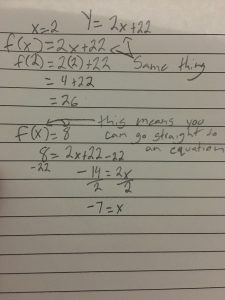This week in math 10 new learned about systems of linear equations. A system of equations is a set of equations that you use all together at once. For example:
4x-y-22=0
2x+2y=6
So you start of by isolating the X or the Y from ether equation
4x-y-22+0 –> 4x-22=y
2x+2y=6 (this stays the same)
then you put the 4x-22 toward where ever a Y is on the other equation
2x+2(4x-22)=6
then you distribute the 2 into the 4x-22
2x+8x-44=6
now you collect like terms and put -44 on the side with the =6 but adding 44 to both sides
10x=50
now you divide and you find x
x=5
To find y, you just need to put the x=5 back into the equation
4(5)-y-22=0 –> 20-y-22=0
isolate the y
y=-2
OR
you can you elimination
4x+2y=6
3x=2y=8
add or subtract the two equations, we want to get two of the terms to cancel out
so in this equation we already have +2y and a -2y so they already cancel out when adding
so when adding we turn out with
7x=14
Divide
x=2
To find y, you once again have to put the x=2 back into one of the equations
4(2)+2y=6 –> 8+2y=6 –> 2y=-2
y=-1