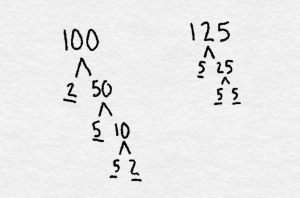In math class we learned how to find the lowest common multiple (LCM) and greatest common factor (GCF) using prime factorization. Essentially prime factorization is all of the prime factors of a number that multiply together to create the whole number.
LCM: Lowest common multiple is a number which 2 numbers can evenly be multiplied to, ex. 4,6. The lowest common multiple of 4 and 6 is 12 (4×3=12) (6×2=12).
GCF: Greatest common factor is a number which evenly divides 2 numbers, ex. 4, 6. The greatest common factor of 4 and 6 is 2 (4/2=2) (6/3=2)
ex. a) 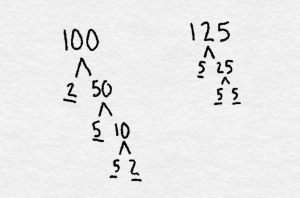 b)
b)
In a) the under lined numbers are all the prime factors, in b) the numbers along the left side of the line are the prime factors. In both a) and b) they show the 2 methods of prime factorization that we learned in class. This step is not showing how to finish finding the GCF or the LCM.
This project wanted us to find a different way aside from prime factorization to solve GCF and LCM.
The method I used to find the greatest common factor and lowest common multiple is by finding and listing all of the divisible factors of the 2 numbers and comparing to see the greatest common factor.
GCF ex.
125: 1 5 25 125
100: 1 2 4 5 10 20 25 50 100
To find the lowest common multiple I took 2 numbers and multiplied them in order starting from 1- 6, although this method doesn’t use prime factorization to do it was still successful.
LCM ex.
125: 250 375 500
100: 200 300 400 500 600 700…
Even with this new method I would still prefer to use prime factorization to figure out LCM and GCF, in my opinion it is easier to find LCM and GCF using prime factorization.