Uses of science cling-Electrostatic dust precopitators
No commentsAdd a comment
Archives: November 2019
Math Project-Riverside Secondary CC
Loading...
Reload document 
Open in new tab S.H. Riverside Secondary CC
Loading...
Everything I know about exponents
2. Describe how powers represent repeated multiplication
Powers are the amount of times the base has to multiplicate itself. For example, if we were to evaluate 23, we would do 2x2x2 because 2 is the base and 3 is the power.
4.Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as 23 and 32.
Having two exponents like 23 and 32 doesn’t mean they will have the same answer. It is not 2×3 and 3×2 which both equal to 6. These are exponents which means that the bases will be multiplicated by themselves to the amount of power so 23 will equal to 8 and 32 will equal to 9.
6.Explain the role of parentheses in powers by evaluating a given set of powers such as (-2)4, (-24), and -24
The powers (-2)4, (-24), and -24 are all determined in different ways. To evaluate (-2)4 you have to do (-2)x(-2)x(-2)x(-2) which equals to 16. (-24), and -24 value the same amount in this example but they can be different when in bigger operations. They are evaluated by multiplication -1x2x2x2x2= -16 which, therefore, gives a different answer than (-2)4. If the negative is not part of the base, it will not be multiplicated with itself and will be counted as a -1 (-1 is a coefficient). The main reason these exponents are different is the negatives.
8.Explain the exponent laws for raising a product and quotient to an exponent.
The exponent laws for raising a product and quotient to an exponent is to multiply the powers and to add it to the bases that do not have powers. For example, If we had (x3y/3y)2 we would have to multiply the powers 2 and 3 to find a single power for x. We would also have to add the power to all the other bases. It would now look like : (x6y2)/(32y2)=(x6y2)/(9y2)=x6/9
Another example:
(x2y5)/(4-2y3)2=(x2y5)/(16y6)=x2/(16y)
10.Use patterns to show that a power with an exponent of zero is equal to one.
*This method works with all bases except 0.
23= 8 33= 27
22= 4 32= 9
21= 2 31= 3
20= 1 30= 1
2-1= 1/2 or 1/21 3-1= 1/3 or 1/31
12. Use patterns to explain the negative exponent law.
22= 4 32= 9
21= 2 31= 3
20= 1 30= 1
2-1= 1/2 or 1/21 3-1= 1/3 or 1/31
2-2= 1/4 or 1/22 3-2= 1/9 or 1/32
14.I can identify the error in a simplification of an expression involving powers.
My example: -(-2)3 + 42 = 8
The mistake in this statement is that the negatives in -(-2)3 have not been evaluated properly. (-2) multiplicated with itself 3 times will be -8 because of the odd power. There is a negative in front of -8 so the answer will be positive. 8 + 16 = 24.
16.Determine the sum and difference of two powers.
42+43=16+64=80 24-22=16-4 =12
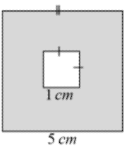
18.Use powers to solve problems (measurement problems)
My example:
=5cm2 – 1cm2
= 25-1
= 24cm2
20.Applying the order of operations on expressions with powers involving negative exponents and variable bases.
My example: y–2x32=9/16
y–2x9=9/16
(1/y2)x9=9/16
9/y2=9/16
y=16
y=4
My partner’s post:
http://myriverside.sd43.bc.ca/jadab2019/2019/11/11/eaverything-i-know-about-exponents/
My CC reflection:
Loading...
A Fresh Look at the Periodic Table-Anita, Ellie, and Sana
DEFINE:
How can we create a periodic table arranged in an organized way? How can we make this table symmetric while having it scientifically correct? Is there a way to make it stand out from the other periodic tables?
DISCOVER:
What are the important categories in the periodic table?
How can our table be easily understood by students?
What are some ideas we can use that are in the periodic table?
DREAM:
Our periodic table shows solids, gases, liquids and founder named elements in easily understandable way. Its based on its state at room temperature. Its shape will be a parallelogram so it looks like a literal table. Its colours are bright against the black poster board. If this periodic table is recognized enough, it might be able to become something more three dimensional like a table made out of wood instead of a poster.
DESIGN:
Our plan is to make a table with four different sections : solids, gases, liquids and founder named elements in an understandable way for students.
DELIVER:
This periodic table is a literal table! It is organized and visually represented in way to educate students our age in an easy way. It is in four different sections, solids, gases, liquids and founder named elements and it is placed by atomic number. It is unique enough to appeal visually and informationally but is also similar enough to the original table to not confuse people.
DEBRIEF:
I could have planned better by organizing my groups time management. Although we all worked on the planning, the final product was not split very evenly and so I had to finish the final product. Even if the time management was not the best, the rest of the project worked out fine. I have learnt a few things while making this table and I know that it will help me through out the rest of my chemistry unit in science.