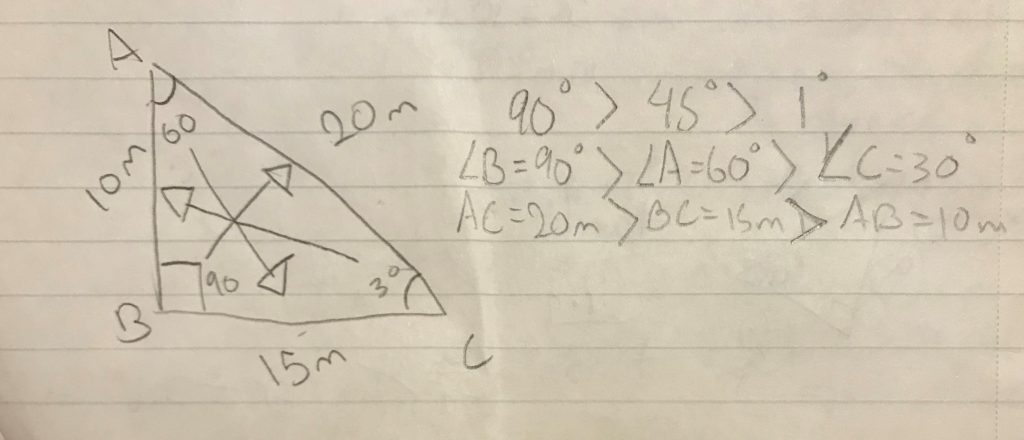https://sd43bcca-my.sharepoint.com/personal/132-mkosola_sd43_bc_ca/Documents/english%2010/literature%20circle%202.docx?web=1

https://sd43bcca-my.sharepoint.com/personal/132-mkosola_sd43_bc_ca/Documents/english%2010/literature%20circle%201.docx?web=1

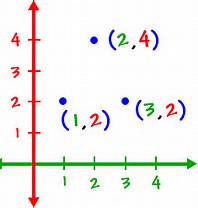
this week in math 10 I learned how to identify if a relation is a function. I learned that for a relation to be a function, it basically means that the input must have only have one output. on  graph, a function would not have any dots sitting directly above each other:

where as in this graph does not represent a function because there are two points vertically above each other

you can also represent functions through mapping diagrams, a mapping diagram uses arrows to connect the inputs with the outputs, an example of a relation that is not a function would be this because 4, as you can see has arrows to three different outputs.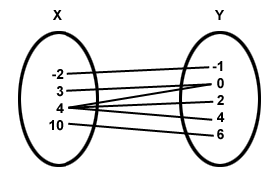

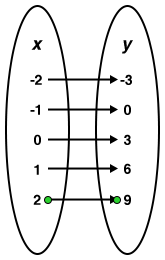
however this diagram represents a function because it is showing that every input number only has one output/one connecting arrow

this week in math 10 I learned how to write an equation for y by looking at a set of numbers and using a T chart. for example this set of numbers:

-5,-2,1,4,7,10,13,16

we would draw out a T chart with the left side as X and the right side as Y. x being the input, y being the output. then under the X we would write 1,2,3,4….. and under the Y we would write our -5,-2,1,4,7,10… now we have to find a rule that will get the X number to the Y number, that will also work for all of the numbers. so 1 to -5, 2 to -2, 3 to 1, 4 to 4, 5 to 7 and so on. we can write the pattern of the numbers along with the starting point  “start at -5 increase by 3 each time.” because its increasing by 3, we multiple 3 with X and then add/subtract a number to get Y. y=3(x)+or-#

replace x with a number 3(1)= 3 and we have to get to -5 so the equation would be 3(1)-8=-5. we can check if 3(x)-8 works for all the pairs of numbers by replacing X and if it does then the rule for this pattern would be 3(x)-8

how to find an angle of a right triangle using trigonometry

this week in math 10 i learned how to make a trinomial that has the “pattern” ( , x, #) look “nicer” if it was written out in a jumbled up order. ex  5x-+40 is written as x, , # rather than   , x, #. so we can write it as – +5x+40 now, the is negative so when we find the greatest common factor, we can take -5 instead of +5 to make it positive, which would also switch the other terms to their opposites, so – +5x+40 is now -5( -x-40)

this week in math 10 I learned that if we have a binomial that says for example, this is considered a perfect square because = (x)(x) , 81= (9)(9). there is no middle term because when factored it would look like (x-9)(x+9), then if you were to expand this back out, the -9 and the +9 would cancel out and become 0, leaving the answer to be a binomial instead of a trinomial. (x)(x)=  + (x)(9)= +9x (-9)(x) = -9x (-9)(9) = -81

+ 9x – 9x -81 .    the +9x and the -9x cancel out to be zero

for this to be a “perfect square” we need to make sure that each term is a perfect square and that the sign is subtraction, not addition

0F69E9B0-5D64-46D9-82F9-08BFFC4ECBF5-1qg30wn

this week we started our unit on polynomials, this was mainly review but i learned how to model binomials multiplied by binomials or binomials multiplied by trinomials or trinomials by trinomials etc, by using an area model. i also learned that you can use this type of model to model more than one digit number multiplication. for modeling polynomials, its all done in a box. if i had ( )(x-5) you would draw a square and divide it into 4 even squares, one for each piece of the expression and along the top you would write then along the side you would write x-5 and you would fill in the box as if it were a multiplication chart so it would look like this….

then you add all of the squares together and combine like terms to get a simplified expression

this week in math 10 I learned how to check that my answers are correct when solving a triangle, so I know that 90⁰ is greater that 45⁰ which is greater than 1⁰, also to remember that the angles in a triangle add up to 180, if my triangle looks like this after ive attempted to solve it:

i need to make sure that angle B is greater than A which is bigger than C, because angleB represents 90 degrees which has to be the largest, angle A represents 60 degrees which would be the second largest, it is between 89 and 45. and angle C would be the smallest because its 30 degrees, between 45 and 1. then the side lengths across from those angles also have to be greatest to smallest in that order.