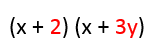One of the things I learned in Math 10 this week is multiplying two binomials. There are a lot of methods to use but the most efficient method is FOIL Method; or First, Outer, Inner, Last.
To do the FOIL method, first, find out if you’re multiplying a polynomial with two terms each. E.g.
![]() So now, we have two binomials that we can multiply. (x + 2)(x + 3y)
So now, we have two binomials that we can multiply. (x + 2)(x + 3y)
How does the FOIL method works? First, you need to know what terms are First, Outer, Inner, and Last.
. So, how do you determine which is which? The first terms are obviously the first terms in each polynomial. In our example it is x and x. The outer terms are the terms ‘outside’ or the ones in both ends of your equation/expression. In our given example, they are the terms x and 3y. The inner terms are the terms ‘inside’ or the two terms in the center of your equation. In our example, they are 2 and x. Lastly, the last terms are the the second terms in each polynomial. It’s 2 and 3y in the example given.
Note: You CANNOT multiply the terms inside of the bracket as they are divided by either addition or subtraction depending on your polynomials.
Continuing the example, (x + 2)(x + 3y), now we need to multiply the binomials. Remember, FOIL