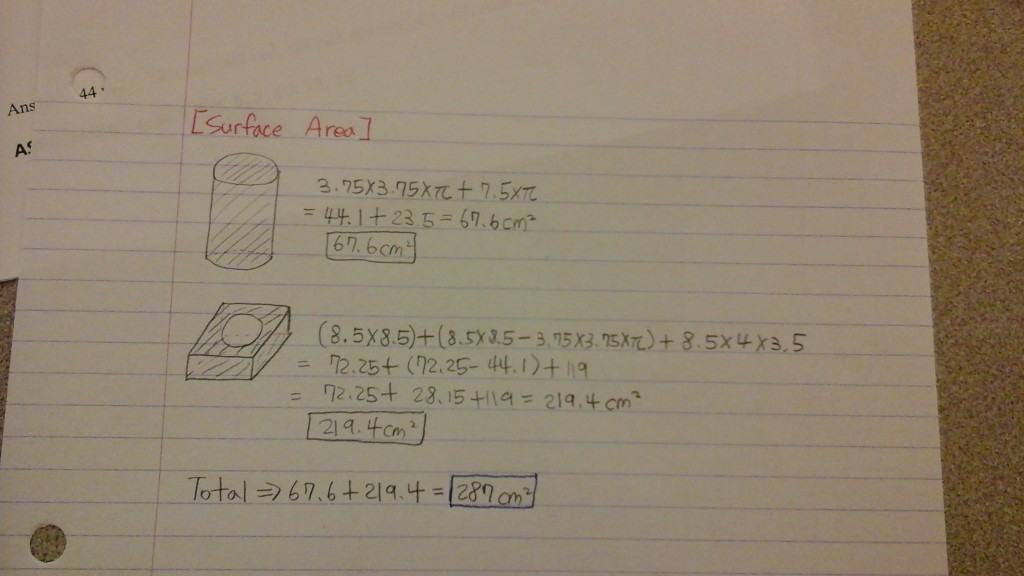We chose 3 bias questions.
Our survey was free and not time sensitive. Our candidates responses were all kept confidential and they all were given the right to refuse to answer. Our questions were asked clearly with an appropriate use of language.
Our preferred method of sampling that we used to collect data was a convenience sample. This is because we asked easy and accessible friends.
We would conduct a convenient sample by surveying students that were more accessible to us. If we conducted a stratified sample we would choose 2 students from all of our classes in our school. To conduct a systematic sample we would choose last names ending in the letter Y off of all our teacher’s attendance list. We would conduct a voluntary response sample by posting our survey on our schools bulletin board
Our survey questions were all revolved around time. Many errors could have been made due to the candidates not knowing the exact time they take to wake up or go to bed and or get ready in the morning. We could have given more multiple choice answers. This way the candidates could have given a more accurate answer. We found that, out of 10 people the majority of the students went to bed at 11 PM, got up in the morning at 6 AM, and spent 30 minutes getting ready in the morning.
–Mean for question 1
Ex. (9+9+11+11+11+11+11+12+12+12) ÷ 10 = 10.9
The average person sleeps at 10:54
–Median for question 2
Ex. 5 6 6 6 6 6 7 7 7 8 (6+6) ÷ 2 = 6
The median of question 2 is 6
–Mode for question 3
The most frequent value occurring in the data is 7.
Math 9
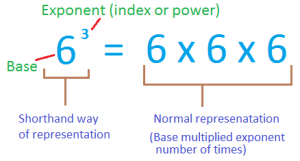
Everything I know about exponents
1) Represent repeated multiplication with exponents
2×2×2 = 2^3
2) Describe how powers represent repeated multiplication
3×3×3×3 – The base is 3 and the exponent is the number of 3’s it has. So 3×3×3×3 is 3^4.
3)Demonstrate the difference between the exponent and the base by building models of a
given power, such as 3 2 and 2 3 .
3^2 : The base is 3 and the exponent is 2
2^3 : The base is 2 and the exponent is 3.
4) Demonstrate the difference between two given powers in which the exponent and the base
are interchanged by using repeated multiplication, such as 3 2 and 2 3 .
3^2 equals to 3×3 and 2^3 equals to2×2×2
5) Evaluate powers with integral bases (excluding base 0) and whole number exponents.
5^2 = 25
6) Explain the role of parentheses in powers by evaluating a given set of powers such as (-2)^4, (-2^4) and -2^4
(-2)^4 = (-2)×(-2)×(-2)×(-2) = 16 (-2^4) = -2×2×2×2 = -16 -2^4 = -2×2×2×2 = -16
7) Explain the exponent laws for multiplying and dividing powers with the same base.
Multiplying powers with the same base : add the exponents
Dividing powers with the same base : subtract the exponents
8) Explain the exponent laws for raising a product and quotient to an exponent.
Product : Keep the base, add the exponents, and if there is a coefficients multiply them.
Quotient : Keep the base, add the exponents, and if there is a coefficients divide them.
If the two bases are different, you divide the bases and subtract the exponents.
9) Explain the law for powers with an exponent of zero.
Whenever the exponent is a zero, the answer is 1.
10) Use patterns to show that a power with an exponent of zero is equal to one.
2^3 = 8 2^2 = 4 2^1 = 2 2^0 = 1
11) I can apply the laws of exponents.
ex) 2^3× 2^9= 2^12
3^5 ÷ 3^2=3^2
(2^3)4=2^12
5^0=1
12) I can identify the error in a simplification of an expression involving powers.
If I know the exponent law corectly, I can identify the error.
ex) 2^3 × 2^4 = 2^12 The answer is wrong because it multiplied the exponents. You have to add the exponents. So the answer is 2^7
13) Use the order of operations on expressions with powers.
To evaluate expressions wig powers in which you have to use BEDMAS.
First you do the brackets first, and if there is a multiplication or a division u have to do that first than addition and subtraction.
ex) (2+3×4) + 2^2= (2+12) + 4=14+4=18
14) Determine the sum and difference of two powers.
Sum : 3^2 + 3^3 = 9 + 27 = 36
Difference : 5^2 – 5^1 =25 – 5= 20
15) Identify the error in applying the order of operations in an incorrect solution.
Wrong way : 3 ×2 + 2^4 correct way : 3×2 + 2^4
= 3 × 18 = 54 =6 + 16=22
17) Use powers to solve problems (growth problems)
Ex) I get 5 dollars a month. How much money do I get after 3months?
1 month : 5 dollars
2 month : 10 dollars (5^2)
3 month : 15 dollars (5^3)
18) Solve problems by applying the order of operations.
Ex) I bought two red pens that each costs 2 dollars and a high liter that costs 1 dollar. 2×2 + 1 = 4+1=5