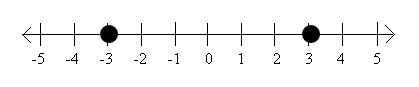Another week, another blog post for Pre-Calc 11!
There were many things that I’ve learned the past week, but one thing we’re going to go over is “completing the square.”
First of all, we have to make sure that our QUADRATIC EQUATION (as explained in the previous blog) is EQUAL to ZERO (0).
Now, let’s do an example here. Let’s say that we have…
(Unfortunately, latex coding isn’t working well this time…)
^ = to the power of.
x^2 + 6x + 8 = 0
Now, what we’re going to do is take the first two terms and make it a perfect square trinomial.
(x^2 + 6x + __) + 8 – __ = 0
So, for this to work, as seen above, we’re going to technically “isolate” the first two terms from the 3rd term and make it a perfect square trinomial. But remember, you can’t just add it like that. Notice that the equation is equal to zero. So this means that you need to have a “zero pair.”
Which means that if you add (let v = ℝ) v from your first two terms, then you must subtract v from the last term.
(x^2 + 6x + 9) + 8 – 9 = 0
So, how did I figure the value for the last term is 9? Here’s the trick.
Divide your middle term by half and square it. So basically if our equation is ax^2 + bx + c, then it will be: (b/2)^2
(x+3)^2 – 1 = 0
So how did we get this? We factor the trinomial (go to my prev blog post for more info) and combined the last two terms.
The next steps should be really straightforward…
(x+3)^2 = 1
Then, just square root both sides. It’ll be:
x+3 = ±√1
x = -3 ±√1