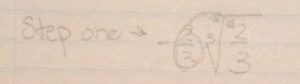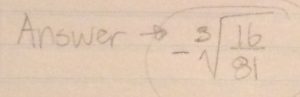This week in Pre-Calculus 11 we learned about multiplying and dividing radicals. I struggled to understand multiplying radical expressions and thought it would be good for this weeks blog post. When you are multiplying radical expressions you need to make sure to use the distributive property.
Equation:
Use the distributive property.
This week in Pre-Calculus 11 we reviewed some math 10 radical work and started to simplify radical expressions. I will be focusing on simplifying radical expressions for this weeks blog post.
Step one-
Bring in the coefficient and leave the negative outside of the radical.
Step Two-
Cube the coefficient that you brought into the radicand.
Step three-
Check for common numbers if there isn’t any multiply the numerators and denominators.
Then you should have your final answer.
.
This week in Pre-Calculus 11 we learned about Geometric Series and how there is finite and infinite Geometric Series. Infinite Geometric Series can be described as converging on a graph. The number continues to get smaller, so you can never really find the sum.
This is the infinite geometric series formula.
Here is an example of infinite geometric series.
We are looking for “r” which is the ratio.
In the first week of Pre-Calculus 11 we learned about Arithmetic Sequences and Series. We learned how to find the sum, a specific sequence number, and how to solve for the general rule for the sequence. I will be showing you how to do all of these in this blog post.
Sequence —> 13, 22, 31, 40, 49…
Formula —> tn = t1 + (n-1)d
Specific Sequence
t50 = ?
tn = t1 + (n-1)d
t50 = 13 + (50-1)7
t50 = 13 + (49)7
t50 = 13 + 441
t50 = 454
General Formula
tn = t1 + (n-1)d
tn = 13 + (n-1)9
tn = 13 + (9n)
Sum of 50 Terms
Formula —> Sn = \frac{n}{2} (t1 + tn)
S50 = ?
S50 = \frac{50}{2} (t1 + t50)
S50 = \frac{50}{2} (13 + 454)
S50 = 25(467)
S50 = 11,675