Author Archives: feliciap2015

One Minute Film

Posted on by
Reply

The specific scenes that we used to portray the theme in our short story give off the important message that The Name Jar emphasizes. The scenes were Unhei feels down on herself and not confident about her name shows how she is wanting to change her identity and pretend to be someone she is not. Her fear of standing out overrides her emotions to such an extent that she allows her classmates to create a jar with names for her to choose. This jar full of American names symbolizes all the identities that aren’t hers and the reason that she hesitates in choosing a name is that none of them suite her. In the scenes with Joey and Mr. Kim, they show her that her name is who she is, and they influence her in a positive way to keep this identity. Furthermore, we found the scene where she was in bus to be very influential in how her fears of being different and not being liked were pushed to a further reality. This then helped her find her identity, though it was a negative experience, by bringing the doubt before bringing comfort in her identity. During this process, we learned to pick out and select out the important scenes that portray the overall message that the author tries to represent. In addition, we learned that we don’t need to display every moment to convey the lesson that needs to be heard and that sometimes simplicity can go a long way.

Blackout Poem – “Death of a Salesman”

Posted on by
1

In English we read a play called “Death of a Salesman” written by Arthur Miller in 1949. “Death of a Salesman” takes place in a post world war society and is about a man name Willy Loman, who is a Salesman, and his daily struggles. These struggles include work, family, dreams, and money. Throughout the play you get to see into Willy’s past and understand him, but also learn some unsettling information about the Salesman. “Death of a Salesman” can be considered a tragedy genre because Willy had worked his entire life for the American Dream. The Dream where the man goes to work and comes home to a doting wife and two kids. Willy had worked so hard to achieve this that he exaggerates about his success, had an affair with another woman, and raised two sons who didn’t know how to properly function in society. All of these factored to his eventual downfall. The blackout poetry project reflects the themes and keywords from “Death of a Salesman.” The poem focuses on the relationship of a father and his family, told through the eyes of one of his kids. Biff’s and Willy’s relationship was very strained because Willy always had high expectations for Biff and expected him to follow in his footsteps, but Willy never let Biff decide what he wanted to do. Willy seemed to be absent from his home and as years dragged on his job affected his mental health, which brought him to his downfall. The poem also contains an illustration of Biff at Willy’s grave while Willy is behind Biff trying to support and connect with him (the swirls connect to his head). On the far right above the grave is Linda. Willy will live on through his wife because she was unquestionably loyal to him and will be in her heart forever (swirls are within her). Willy Loman was not a conventional hero of tragedy, but Miller had made readers empathize for Willy and his situation, so when he arrived at his downfall we would feel his pain and understand.

 

Blackout Poem

Even without Dad.

Eerily quiet.

Intuited what was to come.

Mom rarely expected Dad.

Dad would wonder in late mindless, asleep, and harmless.

Tiptoe off to bed.

Dad his nightmares.

Mom’s undying love.

Dad under a blanket.

 

Week 17 – Trigonometry

Posted on by
Reply

This week in Pre-Calculus 11 we expanded our knowledge on trigonometry. We started off by reviewing Math 10 trig, then moved into unit circles and special triangles. We learned how to do trig without calculators by using special triangles. We reformed SOH CAH TOA to be able to apply it in non-right triangles. Another thing we learned was Sine and Cosine Law.

DOAS Monologues

Posted on by
Reply

The following is an example I created of a monologue for the character Biff from “Death of a Salesman.”

This is a monologue because Biff is talking for a long period of time. This is a monologue because he is talking to Willy.

This monologue would fit into the current plot when Biff, Happy, and Willy are in the restaurant and Willy keeps interrupting Biff. Biff is trying to explain what happened with Oliver

Biff: You are not listening Dad! I am unhappy with the choices I have made in the past several years, so I returned home to this family. I returned from my life on the farm for family and myself even though my own father does not support that life, but still I continued to follow in your footsteps. My entire life my you had supported me especially my football career in High School. I should have tried harder and focused more in school specifically in math class. Mom has been a constant support throughout my life, even though I do sleep around. I went to Oliver like you wanted and he had no idea who I was. My entire life I have felt pressured to follow in your footstep’s and your career. So in the end that’s what I did; I pleased you and mom but sooner or later a man realizes what his true feelings are. I didn’t want or have any interest in a salesman’s career and that is why I stopped going to school and went to a farm. I would never be happy in that firm, I am sorry Dad but I can’t please you anymore.

Week 14 – Multiplying and Dividing Rational Expressions

Posted on by
Reply

This week in Pre-Calculus 11 we started the Radical Expressions and Equations unit. In lesson 7.2 we review multiplying and dividing fractions then learned how to divide and multiply rational expressions.

Example 1:

\frac {24x^3y}{8z^2}\times \frac {2xz^4}{y}

Before simplifying state the restrictions. Restrictions always come from the denominator.

z \neq 0 and y \neq 0

Simplify

\frac {48x^4yz}{8yz^2}

Stop when you can’t simplify any further.

6x^4z^2

 

When multiplying or dividing single variable expressions you need to factor. Factor before stating restrictions because when you factor you can extend trinomials so you have more zeroes. Once the restrictions are stated then you simplify.

How to multiply or divide single variable expressions:

1. Factor

2. State Restrictions

3.Simplify

 

Week 12 – Absolute Value Functions

Posted on by
Reply

This week in Pre-Calculus 11 we started a new unit. This unit includes absolute values and how we can graph them. I will show you how to graph an abosolute value linear function. There are steps that we need to follow when dissecting an equation.

1. Graph the parent function

2. Find the y-intercept

3. Find the slope

4. Graph absolute value

5. Find the critical point (solution)

 

Something to look for when graphing linear absolute value functions is the x-intercept. This is important because the x-intercept is the critical point, the point where the graph changes direction. Some equations will have no solution which means they don’t touch the x-axis.

 

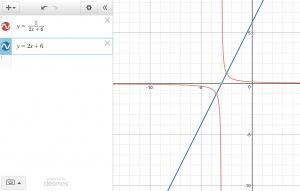
Week 13 – How to graph reciprocal functions

Posted on by
Reply

This week in Pre-Calculus 11 we learned about reciprocal linear and quadratic functions. We learned how to solve the functions algebraically and graphically. My preferred method is graphing to solve because it is a visual for me to see even though it is specific it helps work it out.

How to graph a reciprocal linear function:

1. Graph line (parent function)

2. Plot invariant points (y=1 or y=-1)

3. Asymptotes —> x-intercepts = vertical asymptotes

—> y=0 which is the horizontal asymptotes

 

How to graph a reciprocal quadratic function:

1. Graph parabola (parent function)

2. Invariant points (y=1 or y=-1)

3.Asymptotes —> x-intercepts = vertical (2 possible solutions)

—> y=0 which is the horizontal asymptote