Category: Math 9

Everything Ethan knows about exponents

 

2. Describe how powers represent repeated multiplication

Powers are repeated multiplication, but they are written in a way that is more simple. They are the exact same but mathematicians use 3³ as an easier way to say 3*3*3. The big 3 is the base, or the number multiplied. The small one is the amount of times the base is multiplied by itself.

 

 

 

 

 

4. Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as 2³ and 3².

They are different because in 2³ the 2 signifies the base, and the ³ signifies the number of times the base, or 2, is multiplied by itself. In the second example, 3 in 3² is the base, and the 2 represents the number of times the base (3) is multiplied by itself. 3² or 3×3 (which are the same) ,= 9, so the fact that the numbers are interchanged does not mean that they will have the same product. But, on rare occasions, they can be the same, as seen with 2⁴ and 4² that are both equal to 16. It doesn’t work as regular multiplications as 2 at the power of 3 is 2 times 3 shows up, not 2 times 3.

 

6. Explain the role of parentheses in powers by evaluating a given set of powers such as (-2)⁴, (-2⁴) and -2⁴.

In the first example (-2)⁴, the exponent effects everything inside the parentheses. So, (-2)⁴ will be multiplied by itself 4 times. So, it would be (-2) * (-2) * (-2) * (-2). So, everything, including the negative sign, would be included in the multiplying. The result would be 16.

In the second example, the power is inside the parentheses, so only the 2 would be multiplied by itself 4 times. Then, since the negative sign is not a part of the base, it is left until after the multiplying then applies to the result of the operation, turning it into a negative.

The 3^rd example is the exact same as the afformentioned one, but without the parentheses.

 

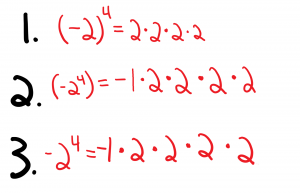
8. Explain the exponent laws for raising a product and quotient to an exponent.

When multiplying 2 numbers that have the same base, at the power of exponents, you can add the exponents to the same base.

When dividing 2 numbers that have the same base, at the power of exponents

 

10. Use patterns to show that a power with an exponent of zero is equal to one.

Exponents with a power of 0 = 1 (n⁰ = 1) unless n = 0, which means there are no numbers at all, so, because it is the multiplicative identity, it equals 1. During this, also get rid of the negative sign in the base. (if it is (-177)⁰, get rid of the negative and it automatically = 1.

 

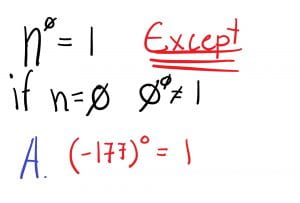
12. Use patterns to explain the negative exponent law.

If you have a negative exponent, then it switches whether it was a numerator or denominator. Say the expression is (-7)^-3. The -3 in the exponents spot means that the -7 becomes a denominator, so it becomes 1/ (-7)³. Right after you put the number underneath (or on top), you get rid of the – sign that’s with the exponent.

Take the base with the same exponent but change the exponent to positive. Let’s call it expression A. Then multiply the original expression by Expression A over Expression A

 

14. I can identify the error in a simplification of an expression involving powers.

The bases for this equation stay the same and the exponents are added, not the bases. So the answer to the mistake would be 5² * 5² = 5⁴.

 

16. Determine the sum and difference of two powers.

2x + x² – x + 3x³ – 2x². Start with the adding of the coefficients of the x. 2x – 1x = 1x. Now add the coefficients related to x². x² – 2x² = -1x². It goes into the negative from 1 to -1. Finally, add the coefficients with x³.With this type of exponents, the bases are x, x², and x³, and the coefficients are the numbers of them. 3x³ is the only one of its kind so it stays as is. End result is 3x³ + x – x².

 

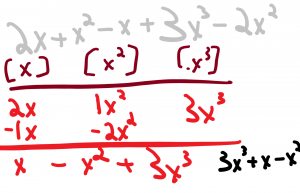
18. Use powers to solve problems (measurement problems)

A guy needs to know his land perimeter for property tax. He knows that his neighbors’ land to the west is 5cm², to the south is 28cm².But, he doesn’t know the area or the side lengths of the property to the east and north.

His neighbors’ properties are (that he knows) are 5m² to the west and 28m² to the south, essentially making his property a triangle. Knowing one of the sides for each of his neighbors’ lawns as 5m and 4m respectively. What is the area of his property and the hypotenuse? The other sides for his neighbor’s lawns are 1m and 7m, so, putting both the correct info into the variables for the Pythagorean Theorem, 5 being a and 7 being b, (5)² + (7)² + (c)². 25 + 49 = 74, which square rooted is 8.60 when rounded to the hundredths spot. So the hypotenuse is 8.6m long.

 

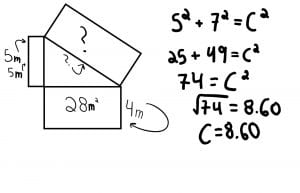
20. Applying the order of operations on expressions with powers involving negative exponents and variable bases.

(3x³y⁴)^-1 (x⁴y²z) / y^-2. The 3 automatically goes on the bottom as it is the only base with an exponent of 1 that is a real number (z is a variable). x^-3 * x⁴ is x^4-3=1, so on top x is at the exponent of 1 so it is alone. The variable y goes: y^2+2-4=0. This means y = 1 and does not need to be included in the final expression. The variable z stays the same the entire time as z is alone and hasn’t anyone on the bottom to socialize with, so it stays on the top as normal. The end product is xz/3.