2. Describe how powers represent repeated multiplication

Powers are the amount of times the base has to multiplicate itself. For example, if we were to evaluate 2³, we would do 2x2x2 because 2 is the base and 3 is the power.

4.Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as 2³ and 3².

Having two exponents like 2³ and 3² doesn’t mean they will have the same answer. It is not 2×3 and 3×2 which both equal to 6. These are exponents which means that the bases will be multiplicated by themselves to the amount of power so 2³ will equal to 8 and 3² will equal to 9. 

 6.Explain the role of parentheses in powers by evaluating a given set of powers such as (-2)⁴, (-2⁴), and -2⁴ 

The powers (-2)⁴, (-2⁴), and -2⁴  are all determined in different ways. To evaluate (-2)⁴ you have to do (-2)x(-2)x(-2)x(-2) which equals to 16. (-2⁴), and -2⁴ value the same amount in this example but they can be different when in bigger operations. They are evaluated by multiplication -1x2x2x2x2= -16 which, therefore, gives a different answer than (-2)⁴. If the negative is not part of the base, it will not be multiplicated with itself and will be counted as a -1 (-1 is a coefficient). The main reason these exponents are different is the negatives.

8.Explain the exponent laws for raising a product and quotient to an exponent.

The exponent laws for raising a product and quotient to an exponent is to multiply the powers and to add it to the bases that do not have powers. For example, If we had (x³y/3y)² we would have to multiply the powers 2 and 3 to find a single power for x. We would also have to add the power to all the other bases. It would now look like : (x⁶y²)/(3²y²)=(x⁶y²)/(9y²)=x⁶/9

Another example:

(x²y⁵)/(4^-2y³)²=(x²y⁵)/(16y⁶)=x²/(16y)

10.Use patterns to show that a power with an exponent of zero is equal to one.

*This method works with all bases except 0.

2³= 8                                                          3³= 27                      

2²= 4                                                          3²= 9

2¹= 2                                                          3¹= 3

2⁰= 1                                                          3⁰= 1

2^-1= 1/2 or 1/2¹                                          3^-1= 1/3 or 1/31

12. Use patterns to explain the negative exponent law.

2²= 4                                                          3²= 9

2¹= 2                                                          3¹= 3

2⁰= 1                                                          3⁰= 1

2^-1= 1/2 or 1/2¹                                          3^-1= 1/3 or 1/31

2^-2= 1/4 or 1/2²                                           3^-2= 1/9 or 1/32

14.I can identify the error in a simplification of an expression involving powers.

My example: -(-2)³ + 4² = 8

The mistake in this statement is that the negatives in -(-2)³  have not been evaluated properly. (-2) multiplicated with itself 3 times will be -8 because of the odd power. There is a negative in front of -8 so the answer will be positive. 8 + 16 = 24.

16.Determine the sum and difference of two powers.

4²+4³=16+64=80                                           2⁴-2²=16-4 =12

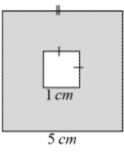
18.Use powers to solve problems (measurement problems) 

My example: 

 

=5cm² – 1cm²

 = 25-1

= 24cm²

 

20.Applying the order of operations on expressions with powers involving negative exponents and variable bases.

My example: y^–2x3²=9/16

y^–2x9=9/16

(1/y²)x9=9/16

9/y²=9/16

y=16

y=4

 

My partner’s post:

http://myriverside.sd43.bc.ca/jadab2019/2019/11/11/eaverything-i-know-about-exponents/

 

My CC reflection: