trigonometry

Pre-Calculus 11 Week 17

alexr2015

This week we covered just about everything in our Trigonometry unit, so I am going to attempt to put as much as I can into this blog post.

SOH CAH TOA is updated for x, y and r. I’ll explain.

Sine = \frac{Opposite}{Hypotenuse} is now sine = \frac {y}{r}

Cosine = \frac{Adjacent}{Hypotenuse} is now cosine = \frac{x}{r}

And Tangent = \frac{Opposite}{Adjacent} is now tangent = \frac{y}{x}

The best way to remember these, is to simply remember that sine is \frac {y}{r}. You should know that the hypotenuse is \frac{x}{r}, so

So where the heck did x, y  and r even come from? Prepare to be introduced to reference angles and unit circles!

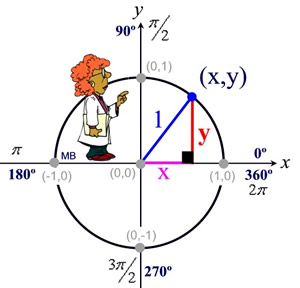
Image result for unit circle trig

Rotation angle is different from reference angle. Rotation angle is how far the terminal arm has rotated from the rest position, 0^o.

Image result for reference angle trig

 

The reference angle is always going to be beside the x-axis. And then from here, we can find out which lines are the

adjacent and opposite lines. Then we can find out which trig ratio to use. For example, the reference

angle for a rotation of 160^o degrees is 20 degrees, because the angle needs 20 more degrees to reach the x-axis. Or, a 225 degree angle has a reference angle of 45 degrees, because it needs to lose 45 degrees to reach the 180 degrees point.

Now, there are special triangles that you should remember as well. These let you do trigonometry without a calculator, and it can also be a way to double check your work.

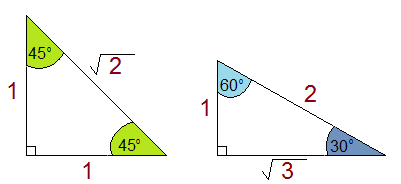
Image result for trig special triangles

Say, you wanted to find sin 45^o. First, you’re dealing with a 45 degree angle, so you know you’re gonna look at your isosceles right triangle. You know sin is \frac{y}{r}, so that means sin45 is \frac {1}{\sqrt{2}}

Or, you want to know cos 60. You know cos = \frac{Adjacent}{Hypotenuse}, or what we’re really supposed to remember, cos = \frac{x}{r}. This means cos 60 = \frac{1}{2}

 

But obviously, you’re not going to deal only with triangles that have side lengths of 1, 2, and \sqrt{3} units.

How do we fix this?

Well, do you remember similar triangles? From grade nine? I’ll refresh you just in case. If two triangles have the same angles, then that means the only difference between the two can be the size, or the side lengths. This means, if you run into another triangle that has angles of 30, 60, and 90 degrees, but has side lengths of 4, 4\sqrt{3} and 8, then you simply have to find the scale factor! The scale factor in that triangle that I described above is 4. If you divide all side lengths by 4, you’ll get our 1-\sqrt{3}$-2 sides again.

Pre-Calculus 11 Week 16 – Trigonometry Review

alexr2015

We finished our Rational Expressions and Equations test this week, so we’ve started our new unit. Trigonometry. So I’m gonna post everything I remember from Trigonometry in grade 10.

Image result for triangle trig

In a right triangle, the side closest to theta that isn’t the hypotenuse is the adjacent side. The side farthest is the opposite side, and the hypotenuse remains the same, like always.

Remember SOH CAH TOA

SOH is Sine = \frac{Opposite}{Hypotenuse}

 

CAH is Cosine = \frac{Adjacent}{Hypotenuse}

 

TOA is Tangent = \frac{Opposite}{Adjacent}

 

To find an angle when you have the lengths of two sides, you can use the inverse of sine, cosine, or tangent. Image result for triangle sidesSay you had this triangle. You want to find the angle of B. Well, that makes the 5cm side the opposite side, and the 7cm side the hypotenuse. We don’t know how long the adjacent side is, so we can’t use that. So which ratio can we use? We can use Sine, because Sine = \frac {Opposite}{Hypotenuse}

So to find the angle of B, we take the inverse sine of 5/7.

 

And of course, with some algebra skills, you can also also find the length of one side if you have the length of another side and an angle.

Don’t forget, you can also use the Pythagorean theorem to find the length of another side if you need to.