How do you graph a quadratic function? It’s the same way you would graph a normal equation. But instead of it looking like a line, it looks like this: 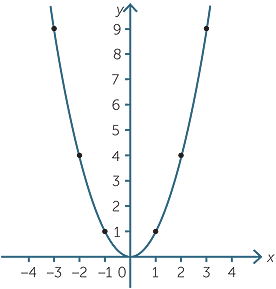
Like, literally, that’s it. That’s all. Just make a table of values, x and y on either side, plug some x values in, calculate for the y values. That’s all. But how bendy and twisty the line is isn’t random. You can spot certain patterns in quadratic functions. Take  for example.
for example.
z represents the scale factor (More on that in a bit), and whether or not the parabola will open up or down. If it opens up, z is positive. If it’s negative, the parabola will open down.
p represents if the parabola moves to the left or to the right of the y-axis. If p is +5, then the parabola’s axis of symmetry, or the middle, will be x = 5. However, this means that in the equation, it’ll appear as  . Because if we remember, a positive and a negative make a negative, so in
. Because if we remember, a positive and a negative make a negative, so in  , it’s actually telling us to translate five units to the right. If our equation was
, it’s actually telling us to translate five units to the right. If our equation was  (Notice the +), then the parabola would be translated 5 units to the left. p also represents the location of the vertex on the x-axis.
(Notice the +), then the parabola would be translated 5 units to the left. p also represents the location of the vertex on the x-axis.
q simply shows us where the vertex lies on the y-axis.
As for z, z is usually 1. If the scale factor is one, the parabola follows a 1, 3, 5 pattern. As in one up, one over. Three up, one over. Five up, one over. And so forth. If the scale factor is 2, then all of that is multiplied by two. Two up, one over. Six up, one over. Ten up, one over. And so forth. Scale factor is 3? Three up, one over. Nine up, one over. Fifteen up, one over. And so forth. So the higher the scale factor is, the thinner the parabola is going to be. The lower, the fatter.
http://amsi.org.au/teacher_modules/Quadratic_Function.html
. Multiplying the denominator by it’s conjugate eliminates the “middle term” that it usually creates. This creates a denominator with no radicals! Proof is below… (Excuse my handwriting)








 Our question is
Our question is 