Day: June 12, 2018

Pre-Calculus 11 Week 17

alexr2015

This week we covered just about everything in our Trigonometry unit, so I am going to attempt to put as much as I can into this blog post.

SOH CAH TOA is updated for x, y and r. I’ll explain.

Sine = \frac{Opposite}{Hypotenuse} is now sine = \frac {y}{r}

Cosine = \frac{Adjacent}{Hypotenuse} is now cosine = \frac{x}{r}

And Tangent = \frac{Opposite}{Adjacent} is now tangent = \frac{y}{x}

The best way to remember these, is to simply remember that sine is \frac {y}{r}. You should know that the hypotenuse is \frac{x}{r}, so

So where the heck did x, y  and r even come from? Prepare to be introduced to reference angles and unit circles!

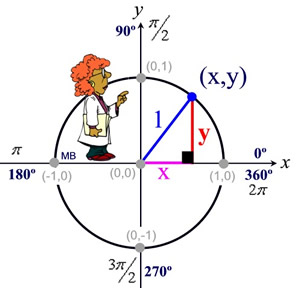
Image result for unit circle trig

Rotation angle is different from reference angle. Rotation angle is how far the terminal arm has rotated from the rest position, 0^o.

Image result for reference angle trig

 

The reference angle is always going to be beside the x-axis. And then from here, we can find out which lines are the

adjacent and opposite lines. Then we can find out which trig ratio to use. For example, the reference

angle for a rotation of 160^o degrees is 20 degrees, because the angle needs 20 more degrees to reach the x-axis. Or, a 225 degree angle has a reference angle of 45 degrees, because it needs to lose 45 degrees to reach the 180 degrees point.

Now, there are special triangles that you should remember as well. These let you do trigonometry without a calculator, and it can also be a way to double check your work.

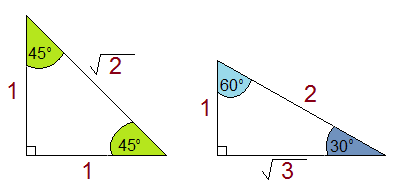
Image result for trig special triangles

Say, you wanted to find sin 45^o. First, you’re dealing with a 45 degree angle, so you know you’re gonna look at your isosceles right triangle. You know sin is \frac{y}{r}, so that means sin45 is \frac {1}{\sqrt{2}}

Or, you want to know cos 60. You know cos = \frac{Adjacent}{Hypotenuse}, or what we’re really supposed to remember, cos = \frac{x}{r}. This means cos 60 = \frac{1}{2}

 

But obviously, you’re not going to deal only with triangles that have side lengths of 1, 2, and \sqrt{3} units.

How do we fix this?

Well, do you remember similar triangles? From grade nine? I’ll refresh you just in case. If two triangles have the same angles, then that means the only difference between the two can be the size, or the side lengths. This means, if you run into another triangle that has angles of 30, 60, and 90 degrees, but has side lengths of 4, 4\sqrt{3} and 8, then you simply have to find the scale factor! The scale factor in that triangle that I described above is 4. If you divide all side lengths by 4, you’ll get our 1-\sqrt{3}$-2 sides again.