This week in Precalculus 11, we learned about Sine Law. You use Sine Law when you have an angle and a side that are opposite from the each other in a triangle.
There are two Sine Law equations:
The first one is for when you’re missing the angle.
The second equation is for when you’re missing the side.
In this example, you need to find the side BC, which is also side a because the angle opposite from it is angle A.
When solving, you can only use 2/3 of the fractions given.
This week in Precalculus 11, we reviewed and learned about trigonometry. We learned about quadrants, the initial arm, the terminal arm, the rotation angle, reference angle, and the coterminal angle. The rotation angle is formed between the initial arm (x-axis on the positive side) and the terminal arm. The reference angle is the angle touching the x-axis and the terminal arm.
*Reference angle can never be over 90°.
Ex.
To find the reference angle, subtract the bigger number with the x-axis number. In this case, you have to subtract 180° from 200° but hypothetically, if the rotation angle was 320°, you would have to subtract 320° from 360°.
To find the coterminal angle, you have to subtract the rotation angle from 360°. In this example, we subtract 200° from 360°. The coterminal angle is negative because it is going the opposite way (clockwise).
This week in precalculus 11, we learned about rational expressions. We learned how to multiply and divide them, add and subtract them, and how to solve them completely. In this post, I will be focusing on the solving aspect.
Note that the equations could result in a linear or quadratic equations and that there are restrictions.
Ex.
The first step is to see if the fractions can factor out.
The next step is to evaluate if you have to multiply by a common denominator or cross multiply.
In this case, we cannot cross multiply since there are 3 expressions, 2 on one side of the equal sign and one on the other, which means that we have to use the multiplying by a common denominator method. you have to multiply the top and bottom of the fractions by the same number(s)/expression(s) (common denominator) and when you multiply the denominator by the same expression, it cancels out.
Common denominator: (x-4)(x+4)
+
= 
(x-4)(x+4)
+ (x+4)
= (x-4)(x+4)
Once the expressions are canceld out, multiply the numerator by the remaining expression, if there is one.
(x+4) + 2(x-4) = 5
From here, you expand, add or subtract like terms, then solve.
x + 4 + 2x – 8 = 5
3x -4 = 5
3x = 9
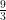
x = 3
State the non-permissable values.
x ≠ 4, -4
This week in precalculus 11, we learned about equivalent reciprocal functions.
Recall that a rational number is a quotient of two integers, except the denominator cannot equal 0. The quotient of two polynomials is called a rational expression.
Equivalent rational expressions: 
When trying to find equivalent rational expressions you factor it out, then simplify it by canceling out the expression that is in the top and bottom of the fraction.
Since the denominator can never equal 0, you have to find the non-permissible values.
Ex.
=
x ≠ -2, -1
With this equation, you can cancel out (x+1) from the top and bottom of the equation.
=
x ≠ -2
This week in Precalculus 11, we learned about Reciprocal Functions.
There are 4 steps to graphing them:
First, graph the linear or quadratic parent function. Once the parent function is graphed, identify the invariant points – which is always 1 and -1 on the y-axis. Next, identify the asymptotes. The horizontal asymptote is always y = 0 and the vertical asymptote is placed at the x-intercept. Lastly, draw the hyperbola, in which you start at the invariant points and draw the lines closer and closer to the asymptotes but never touching or crossing the asymptotes. There are no x-intercepts, as the hyperbolas don’t ever touch the x-axis.
This week in precalculus 11, we learned how to solve systems algebraically. Solving algebraically includes substitution and elimination. In this blog post, I will be going over how to solve systems algebraically by substitution.
To substitute, you have to isolate the variable to one side of the equation. However, this is only done to one of the equations. When the variable is isolated, substitute it for the same variable on the other equation.
Ex.
x – 2y = -10 –> x = 2y – 10
3x – y = 0
3(2y – 10) – y = 0
Once it’s substitued into the other expression, there should only be one variable left in the ecpression. You then solve to find what the variable left in the espression is.
3(2y – 10) -y = 0
6y – 30 – y = 0
5y – 30 = 0
5y = 30
y = 6
Now that you’ve found y, you have to substitute the answer for y back into one of the equations after the variable has been isolated.
y = 6
x = 2y – 10
x = 2(6) – 10
x = 2
The solution is (2, 6).
This week in precalculus 11, we learned how to graph inequalities in 2 variables. When graphing linear inequalities in 2 variables, you need a boundary line and you need to shade one side of the line.
Make sure you know that greater than (>) and less than (<) uses a dotted/broken boundary line and greater than or equal to (≥) and less than or equal to (≤) uses a solid boundary line.
When trying to solve an inequality in 2 variables, you have to isolate y.
Ex.
4x – 2y ≤ -6
-2y ≤ -4x – 6
*When dividing by a negative, you have to flip the sign.
y ≥ 2x + 3
Once y is isolated and you have the slope and y-intercept, you can sketch the graph.
This week in Precalculus 11, we learned about quadratic inequalities and how to solve them. A quadratic inequality is when the equation is greater than 0 (x > 0), greater than or equal to 0 (x ≥ 0), less than 0 (x < 0), less than or equal to 0 (x ≤ 0), or equal to 0 (x = 0).
To solve a quadratic inequality, you have to make sure that one side is zero. If one side is not zero, then you have to move all the numbers to one side to make it zero.
Ex.
4 > x2 – 3x
0 > x2 – 3x – 4
Once all the terms are on one side and the other side is zero, you have to solve for x.
Ex.
0 > x2 – 3x – 4
0 > (x – 4)(x + 1)
x = 4 x = -1
A fast way to find the solution is to imagine a graph and to imagine the x-axis as the 0. We know that the x-intercepts are 4 and -1 and that a is positive, so the parabola will open up. Since 0 is greater than the x’s, we know that we have to find the inequalities for x when it’s above the x-axis. We can now establish that x < -1 and x > 4.
This week in Precalc 11, we learned how to solve my modeling problems. This is solving a word problem by determining the relationships between the variables presented in the problem.
To solve these types of problems, you have to remember that quadratics work for 2 missing variables. Then, determine the variables in the problem and then any other information that the question may be asking. The questions will usually be using terminology like Sum, Product, Greatest, Least, etc. Next, identify the relationship between these variables. This will allow you to solve the rest of the problem. After the relationships are established, you can then solve to produce the answer you’re looking for.
This week in Precalculus 11, we learned about quadratic functions and how to graph them. Quadratic functions are parabolas and they always have 2 variables (usually x and y), a degree of 2, a vertex, a line of symmetry, a domain, and a range. Both an x-intercept and a y-intercept are not mandatory but there usually at least one of them.
The Vertex is the highest or lowest point on the graph. If the parabola opens up, then the vertex is a minimum. If the parabola opens down, then the vertex is a maximum. The line of symmetry is the point where the parabola can be split in half evenly. The x-intercept is when the parabola touches the x-axis and the y-intercept is when the parabola touches the y-axis. The domain is the restrictions for the x-axis and range is the restrictions for the y-axis.
An example of a quadratic function:
y = x2+ x – 6
Since A is positive (1), we know that the parabola opens up and that the vertex is a minimum. We also know that C (-6) is the y-intercept.
To find the x-intercept roots, we have to make y = 0.
0 = x2+ x – 6
It’s now a quadratic equation, not a function, so we can solve for roots.
x2+ x – 6 = 0
(x + 3)(x – 2)
x = -3, 2
x-intercept roots: (-3, 0) and (2, 0)
