Month: April 2018

Week 11 – Quadratic Inequalities with One variable

by victorias2015

Review: 4x-5<11 (you just solve to find x) so 4x<16 => x<4. If diving by negative you must switch sign.

You do the exact same solving for quadratics.

x^2-8x+16>0 Factor= (x-4)^2  then zero product so x=4 then you test a number greater and smaller then 4 in the original equation to see what the restriction is and if the solution is true.

Try 0 (if you can)

0^2-8(0)+16>0 => 16>0 which is true

Try greater number: 5 in this case

5^2-8(5)+16>0 => 1>0 which is also true

 

So the solution/restrictions are x<4 and x>4 to make this quadratic equation true.

Week 9 – Important vocab

by victorias2015

Sum- addition

Product- multiplication

Difference-subtraction

Series and sequences:

Series – the sum of a number of terms

Sequences – pattern of numbers

Arithmetic – common difference (adding or subtracting)

Geometric – common ratio (multiplying or dividing

Appreciates – increasing

Depreciates – decreasing

Finite (geo)- a diverging graph r>1 or r<1 NO SUM

Infinite (geo)- a converging graph -1<r<1

Radicals:

Absolute value- the absolute value of a real number is defined as the principal square root of the squared number

Radicand- is the number the being square rooted

Extraneous solution – the value of the variable doesn’t solve the equation so there is no solution

Polynomials:

Binomial- two terms

Trinomial – 3 terms x^2, x #

Conjugates- they eliminate the middle term ex. (x-9)(x+9) used for perfect square binomials

The zero law – a x b= O a=0 b=0

Restrictions- restrictions are usually needed when finding an isolated variable in radical equations ex. x < 2

Factoring – putting the equation in simpler terms

Solving- finding the value of variables/ the answer

Rational roots- repeats or terminates (factor) whole number, fractions and (+) or (-)

Irrational roots- doesn’t terminate and doesn’t repeat (completing the square)

Real roots- when you solve and can get an answer, x=?

Discriminant – b^2 -4ac, if it’s positive there are 2 solutions, if it’s 0 there is 1 solution and if negative there is no solution

Quadratic:

Minimum graph – opening up

Maximum graph – opening down

Scale of graph – stretch or compressed

Translation- horizontal or vertical

General form- 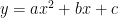y=ax^2+bx+c

Standard form- 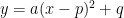y=a(x-p)^2+q

Vertex – change of direction , p,q

Axis of symmetry- c value that divides the graph into 2 equal parts

Domain- x restrictions

Range – y restrictions

 

 

 

Week 9 – General vs. Standard

by victorias2015

The general function is ax^2+bx+c sometimes using this form of the equation is difficult to graph but you can change it to standard form y=a(x-p)^2+q

y=2x^2+4x-5
  1. Take out what’s common (if possible).
y=2(x^2+2x)-5

2. Factor

y=2(x+1)^2-5+1

3. Complete

$latex y=2(x+1)^2-4

This form of the equation gives you more then enough information to graph.

y=a(x-p)^2+q)

P and q are the vertex points (be careful because the p sign will switch from pos to neg or neg to pos), knowing the vertex gives you the axis of symmetry and where the graph starts. A tells you whether the graph will be opening up or down and if it’s stretched or compressed.

 

 

Week 8 – Properties of a Quadratic Function

by victorias2015

All quadratic functions when graphed will have the shape of a parabola either opening up or down.

The parent function is y=x^2 adding different signs and numbers will change the shape and location of the graph. For example the coefficient of x will determine if the graph will be opening up or down. A positive coefficient will make the graph open upward and negative coefficients will make it open downward. This also helps with determine if the graph is a maximum or minimum, if it’s a positive coefficient it will be a minimum graph because it opens upward so the y values will increase on the other hand if it’s negative it would be  maximum graph because the highest y value will be at the top of the downward facing graph. The smaller the coefficient the more the graph will be compressed and the bigger they get the graph will become stretched and skinnier. To find the y intercept look at the end of the parent function y=x^2+3 in this case the y intercept is +3 (just put x value to zero  to find y int) when the point slides up or down it is called a vertical translation. When vertex slides left or right it is called horizontal translation (right or left). y=(x-a)^2 if it’s subtracting a the graph will slide to the right or if it’s adding a it will slide to the left. Other terms used to describe a graph are vertex which is the starting place or change in direction. Axis of symmetry which is the x value the wold split the graph into 2 equal parts. Domain (x values) or range (y values).