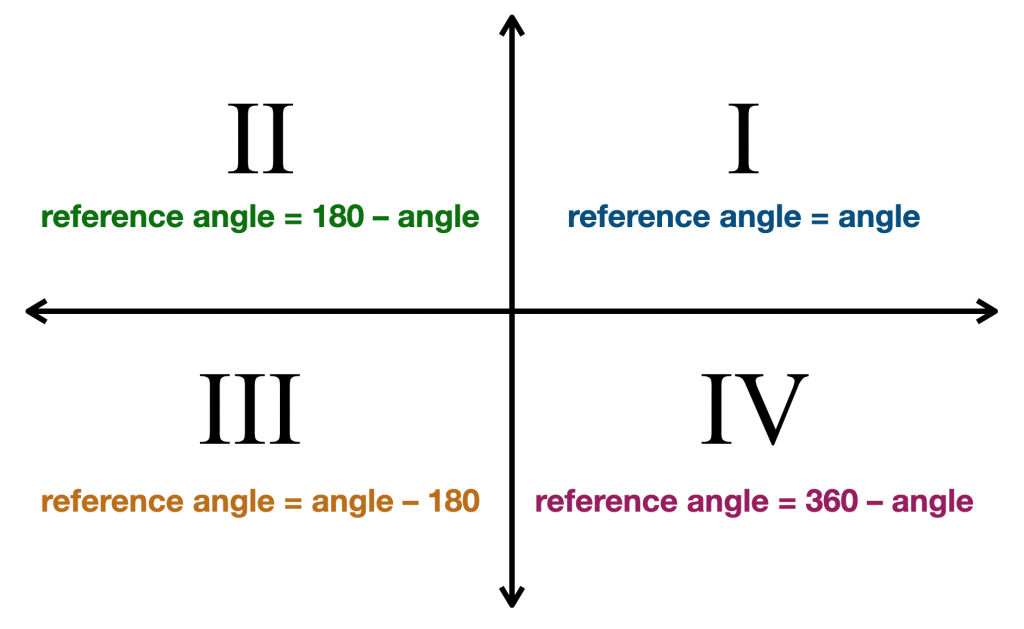
This week in Precalc I choose the rotation angle and refrence angle because the refrence angle was new to me and looked like an angle I had never thought of in math 10. These angles are important because they make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find (x,y)coordinates for those angles.

Steps to Find the Rotation Angle
1. Determine the Quadrant:
– Identify which quadrant the angle lies in based on its degree measure.
– Quadrant I: to
– Quadrant II: to
– Quadrant III: to
– Quadrant IV: to

2. Calculate the Rotation Angle:
– If the angle is between and , it is already a rotation angle.
– If the angle is greater than or less than , subtract or add repeatedly until the angle falls between \(0^\circ\) and \(360^\circ\).

Steps to Find the Reference Angle
1. Identify the Quadrant:
– Use the same quadrant identification as above.

2. Calculate the Reference Angle:
– Quadrant I: The reference angle is the same as the given angle.
–
– Quadrant II: Subtract the angle from .
–
– Quadrant III: Subtract from the angle.
–
– **Quadrant IV**: Subtract the angle from .
–

### Example
Let’s find the rotation and reference angles for .

Rotation Angle
1. **Determine the Rotation Angle*:
– is greater than . Subtract to bring it within the range.
–
– The rotation angle is .

Reference Angle
1. Identify the Quadrant:
– lies on the boundary between Quadrant I and Quadrant II, but it is typically considered to be in Quadrant I.

2. Calculate the Reference Angle:
– Since is in Quadrant I, the reference angle is the same as the given angle.
–

So, for , the rotation angle is \(90^\circ\) and the reference angle is .’

link