I choose dividing Radicals because it is has a unique aspect of it which is rationalizing the denominator. it is important inorder to simplify more complex radical expressions. this can be done by simply dividing the coefficients and radicands by each other but sometimes we are asked to rationalize the denomitor this is a unique way to simplify radicals when dividing and happens when we have a denominator that is a radical we must simplfy it which means not only puting the entire radicals as mixed but also rationalizing the denominator which involves getting rid of radicals from the denominator of a fraction. Here are the steps to do it:
- Identify the Radical: Identify the square root (or other root) in the denominator of the fraction.
- Multiply by the Conjugate: Create a new fraction with the same numerator, but multiply both the numerator and the denominator by the denimator or the conjugate of the denominator expression. we use the conjugate when the dinominator is an expression with atleast two terms which is called a binomial and is obtained by changing the sign between the terms of the radical for example the conjugate for this binomial “
” is this “
“.
- Apply FOIL or Distribution: Multiply the numerator and the denominator using the distributive property (or FOIL if there are two terms) to simplify the expression which just means multiply the first term against the both terms of the other binomial and the same with the second.
 https://study.com/learn/lesson/foil-method-math-overview-examples.html
https://study.com/learn/lesson/foil-method-math-overview-examples.html - Simplify: After multiplying, simplify the resulting expression as much as possible by combining like terms such as the indexs, coefficients and radicands.
- Check for Radicals: Ensure that there are no radicals remaining in the denominator. If there are, repeat the process until the denominator is free of radicals.
By following these steps, you can rationalize the denominator of a fraction effectively.
Example:
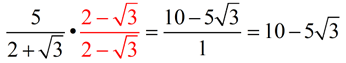
This example has us, use already simplfyied terms so we only have to rationalize the denominator which we do by multiplying both sides by the conjugate of which is
this shows us a difference of squares where the 3rd term so that
gets cancelled out we then get 1 from 4-3 since
=4-3 then we multiply 5 by the conjugate so that the value of the term doesnt change like multipling it by one we then distribute 5 to
so we get
which is are answer in simplest form
