I chose solving Quadratic Equations because they were an interesting application of factoring and grouping and past learning of solving for x. solving Quadratic Equations is important because they allow us to see where linear and non linear lines intersect and define variables in more complex equations.
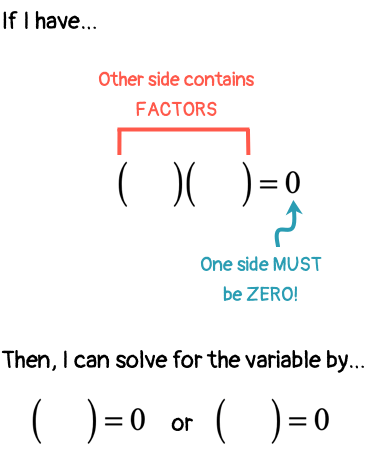
In order to solve a quadratic equation we must identify if an equation is quadratic by seeing if there is a power of 2 and if there is an equals sign. first Write Down the Quadratic Equation:Start with the quadratic equation in standard form: ax^2 + bx + c = 0. where the all the terms are on the side where the variable with an exponent of 2 is positive. Next try to factor the quadratic expression into two binomial factors. This step involves finding two numbers that multiply to give you the constant term (c) and add up to give you the coefficient of the linear term (b) unless the highest power variable has a coefficient higher than one we would do grouping. Once you have factored the quadratic equation, set each factor equal to zero. This creates two separate linear equations. Solve each of the resulting linear equations for the variable x. Check the solutions you found by substituting them back into the original quadratic equation. If they both sides of the equation are equal, they are the correct solutions. Show the solutions in simplest form.
- Write Down the Quadratic Equation: x^2 – 5x + 6 = 0
- Factor the Quadratic Equation: since the coefficient of the highest power variable is one we need to find two numbers that multiply to give 6 and add up to give -5. These numbers are -2 and -3. So, we can rewrite the equation as: (x – 2)(x – 3) = 0.
- Set each factor equal to zero: x – 2 = 0 and x – 3 = 0
- Solve each linear equation: Solving these equations gives us: x = 2 and x = 3.
- Check Solutions: Substitute x = 2 and x = 3 back into the original equation: (2)^2 – 5(2) + 6 = 4 – 10 + 6 = 0, and (3)^2 – 5(3) + 6 = 9 – 15 + 6 = 0. Both solutions satisfy the equation.
- Write Down the Solutions: The solutions are x = 2 and x = 3.
 link
link
