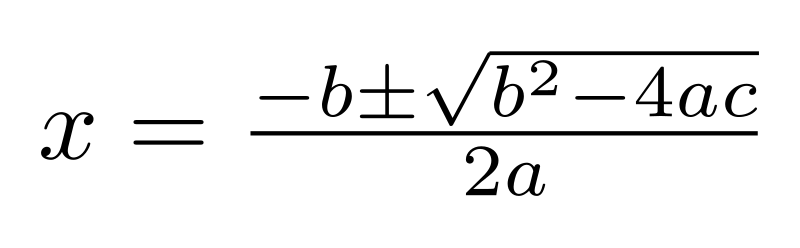Week 8 – Quadratic Functions and Graphs

Posted on April 7, 2018 by shannonf2015

I have learned many things about graphing such as what information we can take out to determine how a graph looks like of a quadratic function. I have also learned the most important information to determine the equation of a quadratic function and how to draw it as a graph.

Parabola: graph of every quadratic function which is a curve

General Form: $y=ax^2+bx+c$

Standard Form: $y=a{(x-p)}^2+q$

Vertex : highest or lowest point; (p,q)

Minimum Point: when the graph opens up (The coefficient next to $x^2$ is positive)

Maximum Point: when the graph opens down (The coefficient next to $x^2$ is negative)

Axis of Symmetry: intersects the parabola at the vertex

Domain : All possible values for x (always the element of real numbers)

Range: All possible values for y

X intercepts: zeros of function (values of x when the function is 0, when y=0)

Pattern of parent function, $y=x^2$ : 1,3,5,7,9…

Throughout the week we have different types of transformations:

Parent Function : $y=x^2$

$y=x^2+q$ : depending on the value of q, the image of the graph $y=x^2$ moves a vertical translation (moves however many times up or down) while keeping the same points, size and just sliding the vertex. This quadratic equation is therefore congruent to the parent function, $y=x^2$ , because it does not change, it just moves up or down.

$y={(x-p)}^2$ : depending on the value of p, the image of the graph $y=x^2$ moves a horizontal translation (however many times to the right or left).

${(x-3)}^2$ —– when the sign is negative, the vertex of the graph moves to the right
${(x+3)}^2$ —– when the sign is positive, the vertex of the graph moves to the left

This is also congruent to the parent function.

$y={ax}^2$ : the graph will stretch vertically when a > 1.

When the value of a is between 0 and 1 (a fraction), the graph will compress vertically : 0 < a < 1

This transformation is not congruent to the parent function.

When these transformations are all combined, the equation becomes standard form.

Let’s look at some examples of using the standard form to determine an equation of a graph.

1) Vertex: look at where the highest or lowest point is and write down the coordinates.

(4,1)

2) Plug in the p and q values from the vertex

$y=a{(x-p)}^2+q$

$y=a{(x-4)}^2+1$

3) Find a point on the graph and use the coordinates to replace x and y.

I’ll use the point : (3, 4)

$4=a{(3-4)}^2+1$

4) Isolate a

$4=a{(3-4)}^2+1$
$4=a(-1)^2+1$
$3=a(-1)^2$
3 = a

The equation is : $y=3(x-4)^2+1$

Let’s look at how we can determine the domain and range and the intercepts by the quadratic function:

Example: $y=3{(x-2)}^2+1$

It is always important to first find the vertex as it is the essential piece of information to be able to determine the form of the graph.

$y=3{(x-p)}^2+q$

Vertex: remember the vertex is (p,q). In our example, p is -2 which becomes +2 because when you place -2 in the standard form, it will become positive with both negatives:

$y=3{(x-(-2))}^2+q$
$y=3{(x+2)}^2+q$

q is the y coordinate of the vertex (not the y-intercept like in general form) which will be 1.

Our vertex is (2, 1)

2. Domain: x∈R – Domain is always the element of real numbers.

3. Range: we should think about the direction of opening to be able to tell the range. Since the coefficient is +3, the graph opens up. This also means that the vertex is a minimum point with y-coordinate 1.

Therefore, y ≥ 1

4. Direction of opening: Opens up

5. Equation of the axis of symmetry: This is the line that cuts through the vertex.

AOS: x = 2

6. The intercepts:

To find the y-intercept, x=0. Replace x with zero in the equation and solve.

$y=3{(0-2)}^2+1$

y = 13

To find the x-intercept, y=0. Replace y with zero in the equation and solve.

$0=3{(x-2)}^2+1$
$-1=3{(x-2)}^2$
$-\frac{1}{3}={(x-2)}^2$

This equation has no solution, so there are no x-intercepts.

Week 7 – Interpreting the Discriminant

Posted on March 18, 2018 by shannonf2015

Last week, we have learned how to determine the number of solutions of a quadratic equation without solving the equation. To be able to do that, we look at the discriminant!

The discriminant is the radicand of the quadratic formula: $b^2-4ac$

This is how to determine the number of solutions by the discriminant.

Two real roots when $b^2-4ac$ > 0

If the discriminant is positive (so greater than 0), it has two solutions. (It touches the x-axis twice)

Exactly one real root when $b^2-4ac$ = 0

If the discriminant is zero, that means there is exactly one solution (Just touches the x-axis once)

No real roots when $b^2-4ac$ < 0

If the discriminant is a negative number (so smaller than 0), it has no solutions (Does not touch the x-axis)

Now that we understand how to use the discriminant to determine the number of solutions, let’s apply these to some equations.

First example: Calculate the value of the discriminant and determine how many solutions.

$4x^2+2x+3=0$

Remember the quadratic equation is : $ax^2+bx+c=0$

Therefore: a = 4, b = 2, c = 3

Plug in the numbers to determine the discriminant.

$b^2-4ac$

$2^2-4(4)(3)$

4-16(3)

4-48

-44

Since the discriminant is negative, it has no solutions; no real roots.

Now let’s look at another example where we have to create an equation with a given number of roots.

Determine the values of y of the equation which has two real roots.

$5x^2+3x+y=0$

To have two real roots, the value of its discriminant must be greater than 0.

So we use: $b^2-4ac$ > 0

Substitute: a = 5, b = 3, and c = y

$3^2-4(5)(y)$ > 0

Simplify.

9 – 20y > 0

Move the 9 to the other side to isolate the variable.

-20y > -9

Divide both sides by -20.

y > $\frac{9}{20}$

Since we divided both sides by a negative number, we must switch the inequality symbol.

y < $\frac{9}{20}$

Week 6 – Solving Quadratic Equations

Posted on March 10, 2018 by shannonf2015

This week, we have learned how to solve quadratic equations by completing the square and applying the quadratic formula when the equation is not factorable.

A quadratic equation includes at least one squared variable and has the following form: ax² + bx + c = 0

a, b and c are constants or numerical coefficients and x is the unknown variable.

Let’s start with the method of completing the squares. This method is quite a long process, it depends on the equation. The best would be to see if it is factorable, if it is not or factoring is too difficult for the equation, you can use the completing the squares method or using the quadratic formula.

Completing the Squares

Lets start with an example:

${x^2}+{4x}=2$

To be able to solve this equation, it must equal to zero as it is a quadratic equation. In this example, we have to move the 2 to the other side so that it becomes zero:

${x^2}+{4x}-2=0$

It becomes -2 because when you move it to the other side of the equation, you switch the signs.

Now that we have it written in the proper equation for us to solve, first check if it is factorable. As there are no numbers that both multiply to equal to two and add to equal 4 (only option is $2\times{1}$ ). So we must use either the completing the squares or formula. In this example, I will be using the completing the squares method.

First, we make two places that are both + and – to get zero pairs in between the inner term and the constant:

Then we find what is the missing constant. To do that, we divide the inner term in two and square it. The answer will be 4. Then we factor for those three terms.

Now that you got ${(x + 2)}^2$ , write the other numbers that are next to it: -4 -2 which equals to -6.

Isolate the variable by moving -6 to the other side of the equation. Then square both sides to get x + 2 = $\sqrt{6}$ . Make sure to include both + and – signs next to the radical because it has two options.

Then move the 2 to the other side of the equation to isolate x.

x = -2 ± $\sqrt{6}$

Now let’s see how we can apply the quadratic formula.

${2x}^2-2x-1=0$

This is the same form as:

${ax}^2+bx+c=0$

a=2, b=-2, c=-1

Formula:

Substitute the variables with the numbers given.

Once you substitute it, simplify it while making sure to keep the + and – sign next to the radical.

Week 5 – Factoring Polynomials

Posted on March 3, 2018March 4, 2018 by shannonf2015

I haven’t really learned much starting this week, but I have learned quite interesting new techniques on factoring polynomials.

Let’s start off with this acronym I have learned to help with the process.

CDPEU – Can Divers Pee Easily Underwater?

Common

Difference of Squares

Pattern

Easy

Ugly

Let’s breakdown what each term means before getting into the factoring process.

Common means find what is common between the terms, the GCF (Greatest common factor).
Difference of Squares means if there are two binomials and they are subtracting.
Pattern means if they have three terms following the pattern: $x^2$ $x$ #
Easy means the easy ones to factor out (straightforward) : $x^2$
Ugly ones are the polynomials that not so straightforward and need more work. We’ll see what method we can use later on. : $a{x^2}$

Now let’s apply these steps!

To start, refer to the list above we just talked about.

The first step is find what is common. To do so, write all the possible factors of both coefficients and see what variables both terms have in common.

After we found all possible factors of 49 and 14, we can see that the common number is 7. Both terms also have at least one x variable. Therefore, you would factor out 7x :

Write out the rest of the values in the bracket next to 7x, making sure when you multiply the values in the bracket with 7x, it will give you the same original expression.

Do we stop here? Well let’s check the list.

Difference of squares is the next one. To tell if it’s a difference of squares, it must have two terms and also be able to form conjugates (subtraction of two terms).

In our example, (7x – 2) does not have an $x^2$ , so we cannot factor them out any further. Therefore, it is not a difference of squares.

Next step is pattern. Well this doesn’t work because it doesn’t have three terms, therefore, we cannot simplify it any further.

It is therefore : 7x(7x – 2)

Now let’s look at an example with three terms.

First step is looking for something in common. As we can see, there’s nothing in common so let’s go to the next step.

Second, is it a difference of squares? No! There is three terms.

So, thirdly, let’s check if there’s the pattern : $x^2$ $x$ #

Yes!

The first thing to do is draw two brackets and start with putting in x to get $x^2$ . Then factor out all the possibilities for 24.

To decide which two numbers we must use for 24, the two numbers that are multiplying must equal to 10 (the inner term) when added together. So the pair to choose would be 6×4. The sign depends on the inner term. It’s positive and so is 24 so therefore we use ++.

This is the final expression factored.

(x + 4)(x + 6)

To check if it’s correct, we can foil back in the values, meaning distribute all the numbers back by multiplying.

So far, these are both easy. But let’s get into the uglier ones.

There are no common factors here, and there are no differences of squares. There is the pattern though with the three terms, but this one seems a little more complicated than the other one we just did.

A method I learned for these ugly trinomials is using the box.

You split a box into four sections, writing in first the value with $x^2$ which in this example is $25{x^2}$ on the top left corner and the constant on the bottom right corner.

We multiply both $25{x^2}$ and 4 which equals to $100{x^2}$ .

Write out all the possible factors of 100 and find which pair adds together to equal to the inner term.

When all values are placed in the box, find the greatest common factor in all the values that are next to each other, not diagonally from each other.

Final thing that I have learned which for me personally is such a life saver, is being able to replace values with variables.

Here is what I mean.

If we are given this example:

We can simply replace (3y + 1) with any variable to make the expression more simple.

Now that we have the expression 2ya – 4a, we need to find the greatest common factor, which is 2a.

Then we have to replace the variable back with 3y + 1.

The final expression factored is: 2(3y + 1)(y – 2).

Week 4 – Simplifying Radical Expressions

Posted on February 24, 2018 by shannonf2015

I learned how to expand and simplify a radical expression.

( $3\sqrt{5}$ + $7\sqrt{8}$ )( $\sqrt{10}$ – $6\sqrt{5}$ )

There are multiply ways of starting to simplify this expression, but the first thing that I do is see if I can simplify the radicals given.

Looking at the expression, I can see that I can simplify $7\sqrt{8}$ , as 8 has a square root, which is 4.

$7\sqrt{8}$ —> $7\sqrt{{4}\times{2}}$ —> $7(2)\sqrt{2}$ —> $14\sqrt{2}$

The next step is to distribute the values in the first bracket and multiply with all the values in the second bracket.

This process is called FOILING.

F – first terms

O – outer terms

I – Inner terms

L – left over terms

Rule: We can simply multiply the radicals together, unlike adding and subtracting where they have to have the same index and radicand.

So in my example, it doesn’t simplify by a lot as they don’t have any like terms.

The answer would therefore be : -90 + $15\sqrt{2}$ + $28\sqrt{5}$ – $84\sqrt{10}$

Since my example isn’t the best to show how to simplify when it comes to like terms, let’s look at this example.

I did this equation in two ways which does give you the same answer. The first way, I simplified the radicals first, then added the like terms together. Note: They have to have the same radicand and same index in order to add them or subtract them together.

The second method, I just added the like terms together first as $4\sqrt{x^3}$ had the same radicand and index as $-7\sqrt{x^3}$ and when you simplify $2\sqrt{x^2}$ , it becomes 2x which can be added with 3x. So when you add the coefficients together keeping the same radicand and index, you are combining like terms.

Then, I simplified the radicals, ${-3}\sqrt{x^3}$ can be simplified to ${-3x}\sqrt{x}$ .

Since we have a variable in our expression, we must define x. Our index here is 2 (square root), therefore, x must be greater than or equal to 0 because we cannot have two numbers that are the same that will multiply to give a negative number: x ≥ 0

Last thing that I have learned was simplifying fractions with a radical as the denominator.

Since we cannot leave radicals in the denominator, we must rationalize the denominator in order to make it a real number.

Rationalizing the denominator means multiplying both the nominator and denominator by the denominator. I included the coefficient but you don’t have to. It would probably be best to just multiply $\sqrt{5}$ with the denominator and nominator, but both give the same results.

After I multiplied them, I noticed I could simplify even more. Then finally, I simplified the coefficients as both can be divide by 10.

Week 3 – Roots and Radicals

Posted on February 18, 2018February 18, 2018 by shannonf2015

I have learned how to simplify radical expressions, as well as changing mixed radicals to entire radicals.

Part 1: How to simplify a radical

$\sqrt[3]{135}$

As we can see, 135 is not a perfect cube root, but we can simplify this radical by finding a cube root that divides into 135.

First let’s look at some vocabulary :

We can see that the index in this example is 3. So the first step is looking through the list that corresponds with the index. In this case it is cube roots.

List of cube roots:

$\sqrt[3]{1}$ = 1

$\sqrt[3]{8}$ = 2

$\sqrt[3]{27}$ = 3

$\sqrt[3]{64}$ = 4

$\sqrt[3]{125}$ = 5

$\sqrt[3]{216}$ = 6

Starting from the top of the list, we can tell that 1 is not going to help, so we move on to the next number which is 8, but that is not a factor of 135 as it doesn’t divide in the number evenly without resulting in a decimal. So we go to the next cube root on the list, which is 27.

27 does divide evenly into 135 which equals 5.

So the radical would look like this :

We can now simplify it by determining the cube root of 27.

$\sqrt[3]{27}$ = 3

That number now becomes the coefficient of the equation and the 5 remains as the radicand :

$\sqrt[3]{135}$ = $3\sqrt[3]{5}$

** Don’t forget to always include the index **

Part 2: How to write a mixed radical as an entire radical.

$2\sqrt[4]{7}$

In this example, we can see that the index is 4, the coefficient is 2 and the radicand is 7.

To be able to turn this into an entire radical, we must be able to put the coefficient (2) back into the root while dragging the index in too.

So we must determine what is $2^4$ and then place that number into the root and multiply both numbers while keeping the index:

Therefore, $2\sqrt[4]{7}$ = $\sqrt[4]{112}$

Week 2 – Geometric Sequences

Posted on February 9, 2018February 13, 2018 by shannonf2015

This past week, I have learned many different formulas and techniques to solve geometric sequences such as finding the sum, a term, and common difference. One of the most important concepts I have learned was how to find a term when given two terms that are not consecutive.

My geometric sequence problem:

In a geometric sequence, the third term is 189 and the sixth term is 5103. Find the eighth term.

Terms:

r = common ratio

a = first term

Step 1: Write down the given values.

$t_3$ = 189

$t_6$ = 5103

$t_8$ = ?

Step 2: Decide which equation would work best with the information given and what info we are missing.

= $t_n={ar^{n-1}}$

As we can see in this equation, we are missing a= $t_1$ and r=common ratio.

To find these values, we must first start by finding r to be able to find the first term.

Since we are given the values for two terms: $t_3$ and $t_6$ , we can find the relation between them in their geometric sequence to find r.

In this image, it shows that to start from the third term, it takes three multiples of the common ratio to get to the sixth term. The equation to find r would look like this:

= $t_3\times{r}^3$ = $t_6$

Now plug in the values given: $t_3$ = 189, $t_6$ = 5103

= ${189}\times{r}^3=5103$

To find r, we must isolate ${r}^3$ . To isolate ${r}^3$ , you must divide 189 on both sides of the equation.

$\frac{189}{189}\times{r}^3={5103}\div{189}$

${r}^3$ = 27

$\sqrt[3]{r}$ = $\sqrt[3]{27}$

r = 3

Step 3: Now that we have the value of r, we can find $t_1$ .

Starting from $t_3$ to go to $t_1$ , we must divide by how many times they are spaced out by the common ratio, as it’s going backwards.

Equation would look like this: $t_3\div{r}^2$ = $t_1$

$189\div{3}^2$ = $t_1$

$189\div{9}$ = $t_1$

21 = $t_1$

Now that we have found $t_1$ and r, we can plug in all the values in the equation.

*We must remember to use Bedmas when solving the equation.*

Back to the equation: $t_n={ar^{n-1}}$

a = 21

r = 3

n = 8

= $t_n$ = $t_8$

= $t_8={(21)(3)^{8-1}}$

= $t_8={(21)(3)^{7}}$

= $t_8={(21)(2187)}$

= $t_8={45 927}$

The eighth term of the geometric sequence is 45 927.

Week 1 – Arithmetic Sequences

Posted on February 3, 2018 by shannonf2015

This is what I have learned so far in the first week of Pre-Calc 11:

My Arithmetic Sequence:

-27, -20, -13, -6, 1

d = 7

d = common difference (In my arithmetic sequence, 7 is being added each time constantly)

Formula : $t_n={t_1+(n-1)}d$

Information that is given:

$t_{1}$ = -27 * $t_{1}$ = first term in a sequence
n (n is the position of term) = 50
d = 7
$t_{n}$ = $t_{50}$
$t_{50}$ = ?

Part 1: How to find : $t_{50}$ (term 50 of the sequence)

Step 1 :

Plug in information that’s given in the formula:

Formula: $t_n={t_1+(n-1)}d$

= $t_{50}={-27+(50-1)(7)}$

Step 2 : Solve

Caution : We have to use BEDMAS when doing the calculations of the formula.

So it would look like this:

= $t_{50}={-27+(49)(7)}$

= $t_{50}={-27+343}$

= $t_{50}={316}$

How to determine general equation of $t_{n}$ :

Step 1: Place given information into formula.

Formula: $t_n={t_1+(n-1)}d$

= $t_n={-27+(n-1)(-7)}$

= $t_n={-27+(-7n+7)}$

= $t_n={-20+(-7n)}$

= $t_n={-7n-20}$

Part 2: Determine the sum of these first 50 terms.

Step 1 :

-27 + -20 + -13 + -6 + 1 } a series

Formula to find the sum : $S_n=\frac{n}{2}{(t_1+t_n)}$

Plug in given information:

$t_{1}$ = -27
n (position of term)=50
$t_{50}$ = 316 <—— we got this answer from finding what is $t_{50}$
$S_{20}$ = ?

= $S_{20}=\frac{50}{2}{(-27+316)}$

Step 2: Solve (BEDMAS)

= $S_{20}={25}{(289)}$

= $S_{20}={7,225}$

Shannon's Blog

My Riverside Rapid Digital Portfolio

Math 11