On this week, I learned Solving Quadratic Equations, Using Square Roots to Solve Quadratic Equations, and Using the Quadratic Formula to Solve Quadratic Equations. Its form is 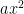 + bx+ c=0
+ bx+ c=0
Solving Quadratic Equations.The zero product property – a*b=0 (x+2)(x-7)=0 x+2=0, x-7=0 x=-2, 7 (2x+1)(3x-5)=0 2x+1=0, 3x-5=0 x=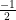 ,
, 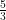
 – 81=0 -> factor (x+9)(x-9)=0 x= 9, -9
– 81=0 -> factor (x+9)(x-9)=0 x= 9, -9  – 90x=0 -> Find a common factor 10x(x-9)=0 x= 0, 9
– 90x=0 -> Find a common factor 10x(x-9)=0 x= 0, 9  -9x -22 = 0 -> factor (x-11)(x+2)=0 x=11, -2
-9x -22 = 0 -> factor (x-11)(x+2)=0 x=11, -2
If the right side of the equation is not equal to zero, so expand the left side. Collect all terms on the left side to get 0 on the right side. Factor the trinomial. Use the zero product property.
ex) (3x+1)(x-6)=22 (3x+1)(x-6)-22=0 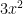 – 7x-6-22=0
– 7x-6-22=0 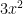 -7x-28=0 -> factor (3x+4)(x-7)=0 x=
-7x-28=0 -> factor (3x+4)(x-7)=0 x=  , 7
, 7
Using Square Roots to solve Quadratic Equations
Solve each equation. Verify the solution
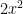 – 1 = 5 -> + 1 each side
– 1 = 5 -> + 1 each side 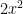 = 6 -> divide 2 each side
= 6 -> divide 2 each side  = 3 -> take the square root of each side x =
= 3 -> take the square root of each side x = 
 – 1 = 5 It is right. This example, a is 1. It is easy but If a is not 1, It will be very complex.
– 1 = 5 It is right. This example, a is 1. It is easy but If a is not 1, It will be very complex.
 +6x -1 =0 -> Multiply each side by -2
+6x -1 =0 -> Multiply each side by -2  – 12 + 2 = 0 -> half of the middle coefficient, then squared it
– 12 + 2 = 0 -> half of the middle coefficient, then squared it  – 12x + 36 – 36 + 2 = 0 -> factor the perfect square
– 12x + 36 – 36 + 2 = 0 -> factor the perfect square  = 34 -> take the square root of each side x-6= +-
= 34 -> take the square root of each side x-6= +-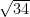 x= 6 ±
x= 6 ±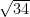
Using the Quadratic Formula to solve Quadratic Equation. In this chapter we have to know Formula. The formula is x=  and a should be not zero. It can be used to determine the solution of any quadratic equation written in the form $latex ax^2 + bx + c = 0
and a should be not zero. It can be used to determine the solution of any quadratic equation written in the form $latex ax^2 + bx + c = 0
 + 2x + 1 = 0 x =
+ 2x + 1 = 0 x =  x =
x =  x=-1+-
x=-1+-


