Tag Archives: burtonpcalc11

End of Year Math Reflection

Posted on by

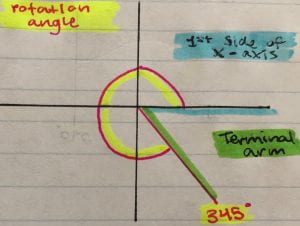
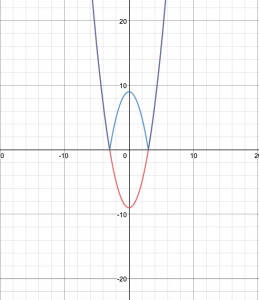
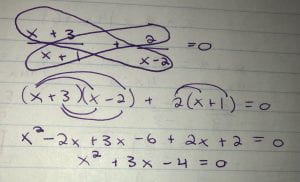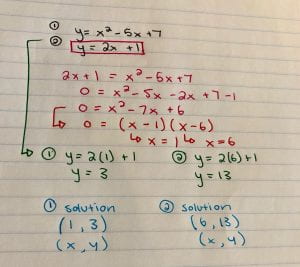Five Things I’ve Learned

  1.  Ask questions.  When stuck ask questions and don’t wait till it’s too late to get help.  If you don’t understand something ask because otherwise, you will continue to be confused.
  2. Finish all your work in your workbook.  When studying for a math test the only way to properly study is to finish all your homework.   I found when I practiced more problems it helped compared to when I left it.  If I understood the concepts enough I wouldn’t complete the work, although the more practice you get is better.
  3. Show up to class.  Things come up and you miss school sometimes, but if you do you miss lessons.  This is something I struggled with.  When missing lessons you have to make it up for it somehow.  Whether coming in early or late to have it taught to you or asking many questions.  These are things I did not do.
  4. Collaborate with friends.  During a week of this semester, I had a table group named table group 5.  I found this table group very beneficial for me because of the people it consisted of.  We always helped each other out and asked questions.  We worked on questions together and no question was a stupid question.  We even made a group chat and face timed one night before a test to study together.  Most of all we had lots of fun and it made the class enjoyable.
  5. Think back to the basics.  When struggling I always thought back to the basics.  For example, what you do to one side you do to the other, if you want to get rid of a square root you have to square it, BEDMAS.  When our struggling during a test your brain is usually freaking out but if you know the basics I find it simplifies things and makes it not as bad as it seems.

Week 18: Precalculus 11

Posted on by

Using the Cosine Law

This week in math we learned how to use the cosine law when solving for an unknown angle.

First, we need to know when we would use the cosine law.   Unlike using the sine law, when we use the cosine law the angle that is given does not usually have a matching length.  As well as, when you use the cosine law there is usually only one angle given rather than two or three.

Our first step to using the cosine law is to know the formula.

Now, we have to put it to use in a equation.  So if this was our triangle:

With what is given in the equation, we just plot into our formula and change the variables if needed.  For our equation we changed the variable of A to Q, B to P, and C to R.  First, solve the square roots of 17 and 23 and then subtract 2(17)(23).  Next, we have to multiple it by Cos 72.  Finally, square each side of the equation so that we get q by itself.

Now, we have just solved for the side length of q.

Week 17: Precalculus 11

Posted on by

Finding a Reference Angle in Standard Position

This week in math we learned how to find a reference angle in standard position.

First to find the reference angle we need to know what the rotation angle is.  The rotation angle is the angle between the first x-axis (rotating counter-clockwise) and the terminal arm is shown below.

A circle is 360 degrees.  So, if we use what we know we need to divide the circle into four quadrants and divide 360 by four.  This gives us reference points.

Now the reference angle is the angle closest to the centre (0,0) and the horizontal axis (X-axis).

Using the reference points we know (where we divided 360 by four) we can easily find the reference angle.  All we have to do is take the nearest horizontal axis reference point this case 180, and subtract our rotation angle which is 120…

…Or if our rotation angle is past 180 we can take our rotation angle which is now 250, and subtract our nearest horizontal axis reference point which in this case is 180.

It’s really that simple.

Week 16: Precalculus 11

Posted on by

Solving Rational Equations 

This week in math we learned how to solve rational equations rather than expressions.

When solving for a rational equation our goal is to determine solution(s) for the variable (x).

If our equation was:

Let’s state the non-permissible values: X cannot be 2, -1, or 0.

Our first step to solving this there is two options; cross multiply or find a common denominator.  You would only be able to cross multiply when the equation includes only two fractions.  In this case, we are able to.

After we cross multiply we need to expand.

After expanding we have to realize whether it is a quadratic or linear equation.  This case it is a quadratic equation.  This means we have to use the zero product law, making one side equal to zero.

Next we have to solve the quadratic, meaning factor it.  This can be done by simply factoring, completing the square, or using the quadratic formula.

After factoring we have found the values for our X variable.  These are our possible solutions and can be checked by verifying them.

Week 15: Precalculus 11

Posted on by

Adding Rational Expressions with Variable Denominators

This week in math we learned how to add rational expressions with variable denominators.

We will start easy so, if our rational expression was:

Our first step when adding rational expressions is to find a common denominator which would be 6x.

When multiplying the denominator to find a common denominator we only multiply the numerator that goes with it.  So in this case we don’t not need to multiply 12  by 2 because the 12 already has a denominator of 6x. We leave that fraction alone.

Now we have to combine like terms.

Finally if you can simplify we simplify otherwise you have your answer.  Notice we aren’t using equal signs because it is an EXPRESSION and expression’s don’t contain an equal sign.

Lastly we need to define the restriction(s) of our variables; X in this case.

Our restriction would be X cannot equal 0.  Because, fractions cannot contain a 0 as the denominator.

 

 

Week 14: Precalculus 11

Posted on by

Absolute Value vs. Reciprocal Function Graphed

This week in math we learned what an absolute value and what a reciprocal function when graphed looks like.

Both have similarities but also many differences.

Both an absolute value graph and reciprocal function graph can either be linear or quadratic.

An absolute value graph looks either like a V or W if quadratic and the graph is never in quadrants 3 or 4 due to the fact it is an absolute value meaning there can be no negatives.  As well as there is critical points. Critical points are the X-intercepts and where the graph starts to reflect. Below are the different types of what an absolute value graph may look like.

Linear:

Quadratic:

On the other hand, a reciprocal function graph if linear has 2 invariant points (0, 1) and (0, -1) and one vertical asymptote which is the X-intercept. If the graph was quadratic it will have 0-4 invariant points and 0-2 asymptotes (X-intercepts).  Both a linear and quadratic reciprocal function graph hyperbolas are created which follow the asymptotes before hitting the invariant points and then follow back to the asymptote. Below are the different types of what a reciprocal function graph can look like.

Linear:

Quadratic:

 

Week 13: Precalculus 11

Posted on by

Solving Absolute Value Equations Using Algebra

This week in math we learned how to solve an absolute value equation using algebra.

Our goal when solving an absolute value equation is to solve for X, the absolute value means X will always be positive.  We know an equation is absolute because it is determined with | signs surrounding the equation.

If our equation was:

We first isolate X to solve for it. Next we take the same equation but multiple it by -1 and solve for X, this is called piecewise notation.

Now that we have solved twice for one equation we take both answers for X and replace it in the equation wherever X is using the original equation (the one you didn’t use piecewise notation on).

After doing this it will determine whether both are solutions, only one, or none.  To keep in mind all answers are not going to be pretty so when solving if you get a fraction keep going with it because although it may not look like something your are used to it may end up turning out correct.

Week 12: Precalculus 11

Posted on by

Solving Quadratic Systems of Equations Algebraically

This week in math I learned how to solve a quadratic system of equations algebraically.

First, we need to know that a quadratic system is similar to a linear system but what makes it different is that it has a degree of two.  Although similarly our end goal is to find the coordinates of the points where each equation intersect with each other.

If my two quadratic equations were:

First I want to get either X or Y by itself.  To do this I must rearrange one of the equations.  In this case, both are already arranged.  I will use the second one because I find it easier to use due to the fact it does not have a square root.

Now that I have Y and is equal to 2x + 1 I will take 2x + 1 and input it into the first equation wherever Y is.

Now I have a quadratic equation that I need to factor.

After factoring I have my X intercepts which are equal to 1 and 6.  To find my values of Y I will take each X intercept and use the first equation and replace X  with my intercepts 1 and 6 to determine it’s Y partner.

Now you have the partners.

Finally you have your two solutions of coordinates of where the quadratic system intersects.

 

Week 11: Precalculus 11

Posted on by

Solving Quadratic Inequalities in One Variable

This week in math we learned how to solve a quadratic inequality in one variable. When doing this in the end we have to make sure the statement stays true.

First to start we have a quadratic inequality as seen below:

Next we have to use the zero product law and make sure there is a 0 on the other side.  In this case this is already done for us.

Now we have to use our factoring rules and factor the following quadratic inequality.  This can be done by simply factoring, using the box, completing the square, or using the quadratic formula.  In this case it is a easy quadratic equation so we can easily factor it:

Now that we know our X intercepts are 2 and 7 we have to test three different numbers. Our first number we will test will be smaller than 2 in this case, the easiest number to choose is 0. Next we will pick a number between 2 and 7, in this example I picked 3 because smaller numbers are easier to deal with. Finally we will pick a number greater than 7 in this case 8, and replace X once more:

Now with the three separate solutions we have we need to create one big solution that stays true to the inequality.  We know that a negative is smaller than a positive so we need to use the signs appropriately while incorporating our X intercepts:

Week 10: Precalculus 11

Posted on by

Math Review

This week in math I reviewed how to simplify an entire radical into a mixed radical.

First we need to know the difference between a mixed and an entire radical.  An entire radical only has a radicand and a mixed radical has a radicand and a coefficient.  As seen below:

To change an entire radical into a mixed one we need to know how to factor.  When factor we take out all the multiples of 2 and once you exterminate multiples of 2 than you move onto three and so on. Here are two examples below:

Finally, if it is a square root you are looking for the pairs that make perfect squares and bringing them outside of the radicand as the coefficient. The number or numbers left over become the radicand.  If there is more than one number left over you simply multiple them together to create that radicand.

Now you have a mixed radical.