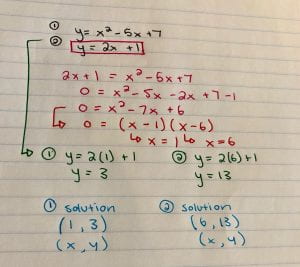The American dream is perceived as a lifestyle that contains no flaws but in fact it is not so flawless. You may think the American dream will solve all your unhappiness but that is not the case. Not only in America do they wish for this dream, but all around the world. An American dream may look like a high paying job, a happy family of four, a steady marriage, financially stable, and big house in the desired location. An American dream is perceived as a perfect life. Although it is perceived as perfect I believe there are many hidden flaws behind the scenes. Portraying life to be perfect causes strains and stress on everything you do. Upholding a persona that is flawless is impossible and with time will break you down. Mentally it will become exhausting and effect not only you but others you interact with. You will not be truly happy. Everyone dreams of the American dream but many don’t realize the imperfections it holds.
Category Archives: Grade 11
Week 12: Precalculus 11
Solving Quadratic Systems of Equations Algebraically
This week in math I learned how to solve a quadratic system of equations algebraically.
First, we need to know that a quadratic system is similar to a linear system but what makes it different is that it has a degree of two. Although similarly our end goal is to find the coordinates of the points where each equation intersect with each other.
If my two quadratic equations were:
First I want to get either X or Y by itself. To do this I must rearrange one of the equations. In this case, both are already arranged. I will use the second one because I find it easier to use due to the fact it does not have a square root.
Now that I have Y and is equal to 2x + 1 I will take 2x + 1 and input it into the first equation wherever Y is.
Now I have a quadratic equation that I need to factor.
After factoring I have my X intercepts which are equal to 1 and 6. To find my values of Y I will take each X intercept and use the first equation and replace X with my intercepts 1 and 6 to determine it’s Y partner.
Now you have the partners.
Finally you have your two solutions of coordinates of where the quadratic system intersects.
Week 11: Precalculus 11
Solving Quadratic Inequalities in One Variable
This week in math we learned how to solve a quadratic inequality in one variable. When doing this in the end we have to make sure the statement stays true.
First to start we have a quadratic inequality as seen below:
Next we have to use the zero product law and make sure there is a 0 on the other side. In this case this is already done for us.
Now we have to use our factoring rules and factor the following quadratic inequality. This can be done by simply factoring, using the box, completing the square, or using the quadratic formula. In this case it is a easy quadratic equation so we can easily factor it:
Now that we know our X intercepts are 2 and 7 we have to test three different numbers. Our first number we will test will be smaller than 2 in this case, the easiest number to choose is 0. Next we will pick a number between 2 and 7, in this example I picked 3 because smaller numbers are easier to deal with. Finally we will pick a number greater than 7 in this case 8, and replace X once more:
Now with the three separate solutions we have we need to create one big solution that stays true to the inequality. We know that a negative is smaller than a positive so we need to use the signs appropriately while incorporating our X intercepts:
Week 10: Precalculus 11
Math Review
This week in math I reviewed how to simplify an entire radical into a mixed radical.
First we need to know the difference between a mixed and an entire radical. An entire radical only has a radicand and a mixed radical has a radicand and a coefficient. As seen below:
To change an entire radical into a mixed one we need to know how to factor. When factor we take out all the multiples of 2 and once you exterminate multiples of 2 than you move onto three and so on. Here are two examples below:
Finally, if it is a square root you are looking for the pairs that make perfect squares and bringing them outside of the radicand as the coefficient. The number or numbers left over become the radicand. If there is more than one number left over you simply multiple them together to create that radicand.
Now you have a mixed radical.
Week 9: Precalculus 11
This week in math we learned how to change an equation that is in vertex form into general form.
Vertex form is also known as standard form. It is important to know how to convert to one another because each equation reveals different components when trying to graph it.
First we need to know what vertex form looks like:
And now this is what general form looks like:
So if my equation in vertex form was:
First I have to square the brackets as a WHOLE and then I have to FOIL the number within. Next, I will take the coefficient out front and multiply what I just foiled. Lastly, I will add like terms. Now it is in general form.
On the other hand, if my equation was in general form I have to complete the square:
First I will divide the middle term by two and then square it. I will create zero pairs by doing this. Finally, I will add or subtract the like terms.
Lord of the Flies Instagram
My Instagram user: piggy3321
This picture and caption relates to when Piggy first saw/met Ralph on the island. This was when they first crashed and were searching for anyone they could find. Piggy first finds Ralph and they exchange names but Piggy only tells Ralph that people at school used to call him Piggy because he is overweight. When Piggy shares this with Ralph, Piggy specifically tells Ralph not to spread the word. Next thing you know Ralph tells Jack along with Jack’s choir boys. This is why he is known as Piggy and I believe this is a big part of the story for Piggy because I shows he is the odd one out and the nerdy one.
This picture and caption relates to how Jack always thought he should be chief rather than Ralph. This picture portrays Jack and his choir boys with their spheres, only wanting to hunt pigs rather than building important things like shelters or fires. Piggy was very focused on surviving and had many good ideas when it came to trying to get rescued. Piggy’s caption shows how he disagrees with Jack.
This picture relates to Simon who was killed by Jack and the rest of them. Simon was one of the only civil ones left, including Piggy. So, Piggy posted this picture in memory of him. Even though Piggy was involved in the murder, Piggy is paying his respects and realizes how wrong it was.
This picture relates to when Jack decided to leave to make his own group and just hunt pigs. Piggy gained more confidence after this moment in the book and I feel as if he had refocused and felt more hopeful since Jack was gone, and Jack would never let Piggy say a word. Now Piggy has a voice.
This relates to when Piggy first met Ralph and Piggy found the conch and knew that if you blew n it, it created a loud noise. This was the turning point of the whole story because Piggy telling Ralph how to use it summoned a group of kids from the forest.
This post is supposed to represent how intelligent Piggy is. Piggy had many great ideas and was not always listened to. He suggested there is no beast but if they were so scared why not build the fire on the beach? He had many solutions to problems and this is why Piggy was such a pivotal character.
The post below shows Jack and Piggy’s relationship. Jack breaks Piggy’s glasses for no reason and expects that Piggy will continue to want to help. Piggy is too insecure to stand up for himself so e just goes with the flow. Throughout the book Piggy is always treated unfairly by Jack. Ralph soon realizes this and Piggy and Ralph become close friends.
Week 8: Precalculus 11
Standard Form of a Parabola Equation
This week in math we learned about the standard form of a parabola equation.
When using the standard form of the equation it is very useful because it reveals a lot about how to graph the equation without a table of values.
First of all, standard equation is: y = a
At first glance, it looks very confusing but with the information we have you are able to found out the directions opening, vertex, axis of symmetry, intercepts, domain, and range. Some information is found easily by just looking at the values that correspond with the variables but in some cases, the information you will have to be pieced together.
When looking at y = a
A, whether the parabola opens up or down and if the vertex is a maximum or minimum vertex. If the value of a is negative than the parabola opens down and we know the vertex will be at its maximum. If the value is positive then we know the parabola opens up and the vertex will be at its minimum.
P, tells you the horizontal translation. Also known as to when starting at 0 on the x-axis if you will be sliding left or right. Another thing to note is if the p-value follows a positive you will be sliding to the left (negative) by that many intervals and if the p-value follows a negative you will be sliding to the right (positive) by that many intervals. It will always be the opposite value.
Q, tells you the vertical translation. Also known as to whether you’ll be going up or down from the horizontal translation. If the q-value is negative you will be moving down by the amount of q and if the q-value is positive you will be moving up by the amount of q.
Now using this information we can piece it together to find the vertex, axis of symmetry, intercepts, domain, and range.
Taking our horizontal and vertical translations we can determine the vertex. The p-value will be the value of the vertex and the q-value will be our y-value of our vertex. Now that we have our vertex we now know our axis of symmetry. Our line of symmetry is just the horizontal translation or our x-value of the vertex. The axis of symmetry is the line that splits the parabola symmetrically in half.
Our domain will always be x = all real numbers and our range will be y >/= or </= to the y value of our vertex. So, if the vertex is at its minimum then y >/= (y vertex value). And if the vertex is at its maximum then y </= (y vertex value). In this case above y >/= 3.
Week 7: Precalculus 11
Discriminant
This week in math we learned about discriminants.
The discriminant is 
Now that we know what the discriminant formula we need to know what the variables stand for. If I had a quadratic equation of…
A = 3, B = 4, C = 2.
Now we take the discriminant and then replace each variable with the corresponding number…
Then we solve…
Finally, if the number under the square root sign is less than 0 this means there is no solution or real roots. If the number under the square root is equal to 0 this means there is only one solution and really root and lastly, if the number is greater than 0 there is two solutions and two real roots.
In this case, the number under the square root is -8 which is less than 0 so this means, there is no solution or real roots to this quadratic equation.
Using the discriminant is helpful because we can determine how many solutions or real roots there are without solving the quadratic equation.
Week 6: Precalculus 11
Zero Product Law
This week in math we learned the zero product law.
The zero product law makes it easy and helps us when we are trying to solve quadratic equations. The basics of zero product law is when, a -b = 0 then, a or b must equal 0.
At first I was confused about what a quadratic equation was and the difference between one and a linear equation. Something that helps me understand the difference is that linear equations do not include exponents.
If my equation was 
From here using the zero product law (a -b = 0 then, a or b must equal 0.) I have to find two numbers to replace x in this case that will equal to 0 when added or subtracted by 9.
When I look at (x – 9) I know that x has to be 9 because 9 – 9 = 0. For when I look at (x + 9) I know in the end it has to equal to 0 so, I know x has to equal -9 because -9 + 9 =0.
Finally, I have one x equal to 9 and the other equal to -9. Now to verify I can replace x with either -9 or 9 to check if only one or both solutions work. In this case, both solutions work because as long as one of your terms is equal to 0 it will be multiplied by the other and anything multiplied to 0 is 0.
Week 5: Precalculus 11
Factoring Polynomials
This week in math we learned how to factor polynomials.
Factoring polynomials were first introduced in grade 10 and now we are expanding our knowledge. To understand how to factor a polynomial we were introduced to an acronym CDPEU, these letters stand for:
COMMON: is there anything common throughout the whole polynomial that divides evenly?
DIFFERENCE OF SQUARES: does anything have a relationship with a perfect square, which allows you to use conjugates?
PATTERN: is it a trinomial? Do the variable as well as finding two numbers that are factors of the product and add or subtract to the middle number?
EASY: are the coefficients easy to deal with?
UGLY: is the first coefficient greater than one? (You will have to use the box method, or guess and check)
When factoring a polynomial if you go through each of these letters and their meaning and then ask yourself if they relate to the polynomial you are trying to solve it makes solving polynomials a lot easier.
So, if the polynomial I had to factor was:
Then I would ask myself if there is anything common? In this case, no. Then I would ask myself if it is a difference of squares? Meaning you are easily able to square rot each number, in this case, no as well. Next, I need to ask my self if there is a pattern. My answer to that is yes, there is a pattern.
Now, I know X will be in each component since the polynomial includes an X squared.
Next, I have to find factor 14 and out of those factors find two numbers that add to 9. In this case, those two numbers are 2 and 7.
Finally, I have to pay attention to the negatives and positives. In this case, all are positive so I don’t have to worry.
In the end, it should look like this:
But, if 9 was negative this means that both factors, 2 and 7 must be negative. But, if 14 was also negative, 7 must be negative since there would be more negatives then positives and 7 is greater than 2.
Now you know how to solve polynomials through the method using the pattern.