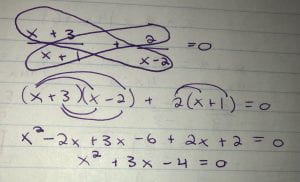To better understand the world and get out of my comfort zone I can say yes to more opportunities. This allows for more experiences whether they are positive or negative experiences I will always learn something new. Through these opportunities it may allow me to meet more people, see new things, try new things. It allows you to create your own opinion about the world rather than following the status quo.
Category Archives: Grade 11
End of Year Math Reflection
Five Things I’ve Learned
- Ask questions. When stuck ask questions and don’t wait till it’s too late to get help. If you don’t understand something ask because otherwise, you will continue to be confused.
- Finish all your work in your workbook. When studying for a math test the only way to properly study is to finish all your homework. I found when I practiced more problems it helped compared to when I left it. If I understood the concepts enough I wouldn’t complete the work, although the more practice you get is better.
- Show up to class. Things come up and you miss school sometimes, but if you do you miss lessons. This is something I struggled with. When missing lessons you have to make it up for it somehow. Whether coming in early or late to have it taught to you or asking many questions. These are things I did not do.
- Collaborate with friends. During a week of this semester, I had a table group named table group 5. I found this table group very beneficial for me because of the people it consisted of. We always helped each other out and asked questions. We worked on questions together and no question was a stupid question. We even made a group chat and face timed one night before a test to study together. Most of all we had lots of fun and it made the class enjoyable.
- Think back to the basics. When struggling I always thought back to the basics. For example, what you do to one side you do to the other, if you want to get rid of a square root you have to square it, BEDMAS. When our struggling during a test your brain is usually freaking out but if you know the basics I find it simplifies things and makes it not as bad as it seems.
Week 18: Precalculus 11
Using the Cosine Law
This week in math we learned how to use the cosine law when solving for an unknown angle.
First, we need to know when we would use the cosine law. Unlike using the sine law, when we use the cosine law the angle that is given does not usually have a matching length. As well as, when you use the cosine law there is usually only one angle given rather than two or three.
Our first step to using the cosine law is to know the formula.
Now, we have to put it to use in a equation. So if this was our triangle:
With what is given in the equation, we just plot into our formula and change the variables if needed. For our equation we changed the variable of A to Q, B to P, and C to R. First, solve the square roots of 17 and 23 and then subtract 2(17)(23). Next, we have to multiple it by Cos 72. Finally, square each side of the equation so that we get q by itself.
Now, we have just solved for the side length of q.
Week 17: Precalculus 11
Finding a Reference Angle in Standard Position
This week in math we learned how to find a reference angle in standard position.
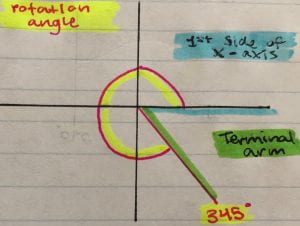
First to find the reference angle we need to know what the rotation angle is. The rotation angle is the angle between the first x-axis (rotating counter-clockwise) and the terminal arm is shown below.
A circle is 360 degrees. So, if we use what we know we need to divide the circle into four quadrants and divide 360 by four. This gives us reference points.
Now the reference angle is the angle closest to the centre (0,0) and the horizontal axis (X-axis).
Using the reference points we know (where we divided 360 by four) we can easily find the reference angle. All we have to do is take the nearest horizontal axis reference point this case 180, and subtract our rotation angle which is 120…
…Or if our rotation angle is past 180 we can take our rotation angle which is now 250, and subtract our nearest horizontal axis reference point which in this case is 180.
It’s really that simple.
Too Late…
There lived a man. He was an ordinary man. Though, he lived his life with great expectations. Expectations that felt pressured from not only himself but from society, his family and friends. He wanted to be the best possible version of himself; perfect. Little did he know what he was doing to himself. Deteriorating himself slowly from the inside out. It all started when he was young. Wanting to be the popular kid, someone everyone would look up too. Portraying a persona that was addictive to society. A persona the people would favour. He had forgotten about his morals and values or perhaps never found them. Little did he know he was slowly deteriorating himself. Next, came his teenage years. Pressuring himself to live up to his popularity while getting good grades. Ultimately, so his parents would be proud and the people would look up to him. He began to fall off the wagon, failing all his classes. Pressuring himself to a point where he felt helpless, confused, and empty inside. Little did he know he was deteriorating. His feelings and touch with reality had vanished from him. All that was left was his appearance. Finally, he grew up to be an adult. Feeling lost and clueless to the reality around him he had no career, the only thing getting him through life were his friends. His friends were always there for him throughout his whole life, though he was unaware of the support. Focused on pleasing expectations all his life. He did not realize the importance of what he had. Little did he know he had already deteriorated. He was empty and now he had no appearance. As if he was invisible he didn’t know who he was anymore. Until one day he had enough. He opened his eyes and realized life was more. It was about cherishing relationships, being kind, and finding something that makes you happy. Not popularity, your success, or numbers. However, he was too late, and now he is gone.
Week 16: Precalculus 11
Solving Rational Equations
This week in math we learned how to solve rational equations rather than expressions.
When solving for a rational equation our goal is to determine solution(s) for the variable (x).
If our equation was:
Let’s state the non-permissible values: X cannot be 2, -1, or 0.
Our first step to solving this there is two options; cross multiply or find a common denominator. You would only be able to cross multiply when the equation includes only two fractions. In this case, we are able to.
After we cross multiply we need to expand.
After expanding we have to realize whether it is a quadratic or linear equation. This case it is a quadratic equation. This means we have to use the zero product law, making one side equal to zero.
Next we have to solve the quadratic, meaning factor it. This can be done by simply factoring, completing the square, or using the quadratic formula.
After factoring we have found the values for our X variable. These are our possible solutions and can be checked by verifying them.
Week 15: Precalculus 11
Adding Rational Expressions with Variable Denominators
This week in math we learned how to add rational expressions with variable denominators.
We will start easy so, if our rational expression was:
Our first step when adding rational expressions is to find a common denominator which would be 6x.
When multiplying the denominator to find a common denominator we only multiply the numerator that goes with it. So in this case we don’t not need to multiply 12 by 2 because the 12 already has a denominator of 6x. We leave that fraction alone.
Now we have to combine like terms.
Finally if you can simplify we simplify otherwise you have your answer. Notice we aren’t using equal signs because it is an EXPRESSION and expression’s don’t contain an equal sign.
Lastly we need to define the restriction(s) of our variables; X in this case.
Our restriction would be X cannot equal 0. Because, fractions cannot contain a 0 as the denominator.
Week 14: Precalculus 11
Absolute Value vs. Reciprocal Function Graphed
This week in math we learned what an absolute value and what a reciprocal function when graphed looks like.
Both have similarities but also many differences.
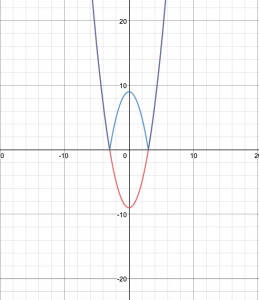
Both an absolute value graph and reciprocal function graph can either be linear or quadratic.
An absolute value graph looks either like a V or W if quadratic and the graph is never in quadrants 3 or 4 due to the fact it is an absolute value meaning there can be no negatives. As well as there is critical points. Critical points are the X-intercepts and where the graph starts to reflect. Below are the different types of what an absolute value graph may look like.
Linear:

Quadratic:
On the other hand, a reciprocal function graph if linear has 2 invariant points (0, 1) and (0, -1) and one vertical asymptote which is the X-intercept. If the graph was quadratic it will have 0-4 invariant points and 0-2 asymptotes (X-intercepts). Both a linear and quadratic reciprocal function graph hyperbolas are created which follow the asymptotes before hitting the invariant points and then follow back to the asymptote. Below are the different types of what a reciprocal function graph can look like.
Linear:

Quadratic:
Week 13: Precalculus 11
Solving Absolute Value Equations Using Algebra
This week in math we learned how to solve an absolute value equation using algebra.
Our goal when solving an absolute value equation is to solve for X, the absolute value means X will always be positive. We know an equation is absolute because it is determined with | signs surrounding the equation.
If our equation was:
We first isolate X to solve for it. Next we take the same equation but multiple it by -1 and solve for X, this is called piecewise notation.
Now that we have solved twice for one equation we take both answers for X and replace it in the equation wherever X is using the original equation (the one you didn’t use piecewise notation on).
After doing this it will determine whether both are solutions, only one, or none. To keep in mind all answers are not going to be pretty so when solving if you get a fraction keep going with it because although it may not look like something your are used to it may end up turning out correct.
Self-deception
I think that John and Emily have potential to achieve everything they want to achieve and if they are willing to do it. They will have to make big sacrifices but it is able to get done. Although, they may be capable physically to do this how about mentally and is it realistic?
Finding the proper balance between social, school, sports, and family is extremely hard when they are following a schedule as busy as they are. From experience I definitely understand this scenario as I am writing this waiting for my flight. If you/John and Emily do not find the proper balance with their busy schedule, after time mentally they will not be able to handle it. They will get stressed and can get unmotivated to finish a job they may have started.
If not finishing their English assignment I believe they will blame themselves but as well as others that were involved. They will be disappointed that they were incapable of finishing, but they will also for example blame their teacher for assigning the assignment.
Funny thing is I feel like I am in their place. I am in Richmond four times a week and stay til 10 at night for practice. Its extremely hard finishing my homework when I also have such heavy course load and don’t understand it all. Meanwhile, I only have one free day on the weekend which I don’t think a lot of teachers understand. I definitely am stressed almost 24/7. It is important to find balance but at times it seems nearly to impossible. Its very bad for your mental health. So, my advice for John and Emily is take a step back and be more real with yourself whether you can complete a task you take on or not.